题目内容
5. 某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.
某货运公司规定,从甲城到乙城的计价标准是:40吨以内100元(含40吨),超出40吨的部分4元/吨.(1)写出运费y(元)与货物重量x(吨)的函数解析式,并画出图象;
(2)若某人托运货物60吨,求其应付的运费.
分析 (1)利用条件:40吨以内100元(含40吨),超出40吨的部分4元/吨,可得分段函数;
(2)x把x=60代入40x-60得结论.
解答 解:(1)根据40吨以内100元(含40吨),超出40吨的部分4元/吨,
可得分段函数$y=\left\{\begin{array}{l}100,0<x≤40\\ 4x-60,x>40.\end{array}\right.$…(4分),
如图所示;
(2)把x=60代入40x-60得,运费为180元.
点评 本题考查函数模型的建立,考查利用数学知识解决实际问题,考查学生的计算能力,属于中档题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
16.已知A(-1,0),B(3,0),则与A距离为1且与B距离为4的点有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
20.在空间中,下列命题正确的是( )
| A. | 经过三个点有且只有一个平面 | |
| B. | 经过一个点和一条直线有且只有一个平面 | |
| C. | 经过一条直线和直线外一点的平面有且只有一个 | |
| D. | 经过一个点且与一条直线平行的平面有且只有一个 |
17.若函数f(x)在其定义域的一个子集[a,b]上存在实数m(a<m<b),使f(x)在m处的导数f'(m)满足f(b)-f(a)=f'(m)(b-a),则称m是函数f(x)在[a,b]上的一个“中值点”,函数$f(x)=\frac{1}{3}{x^3}-{x^2}$在[0,b]上恰有两个“中值点”,则实数b的取值范围是( )
| A. | $(\frac{2}{3},3)$ | B. | (3,+∞) | C. | $(\frac{3}{2},3)$ | D. | $({\frac{3}{2},3}]$ |
14. 执行如图所示的程序框图,若输出的结果为80,则判断框内应填入( )
执行如图所示的程序框图,若输出的结果为80,则判断框内应填入( )
 执行如图所示的程序框图,若输出的结果为80,则判断框内应填入( )
执行如图所示的程序框图,若输出的结果为80,则判断框内应填入( )| A. | n≤8? | B. | n>8? | C. | n≤7? | D. | n>7? |
15.设a∈R,“a>0”是“$\frac{1}{a}>0$”的( )条件.
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充要 | D. | 既非充分也非必要 |
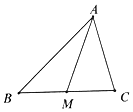 如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.
如图,锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,点M为BC的中点.