题目内容
18.抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足$∠AFB=\frac{π}{3}$,设线段AB的中点M在l上的投影为N,则$\frac{{|{MN}|}}{{|{AB}|}}$的最大值是1.分析 设|AF|=a,|BF|=b,连接AF、BF.由抛物线定义得2|MN|=a+b,由余弦定理可得|AB|2=(a+b)2-3ab,进而根据基本不等式,求得|AB|的取值范围,从而得到本题答案.
解答 解:设|AF|=a,|BF|=b,连接AF、BF,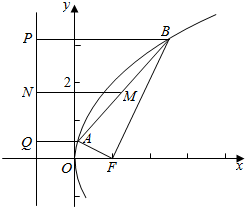
由抛物线定义,得|AF|=|AQ|,|BF|=|BP|,
在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b.
由余弦定理得,
|AB|2=a2+b2-2abcos60°=a2+b2-ab,
配方得,|AB|2=(a+b)2-3ab,
又∵ab≤$(\frac{a+b}{2})^{2}$,
∴(a+b)2-3ab≥(a+b)2-$\frac{3}{4}$(a+b)2=$\frac{1}{4}$(a+b)2
得到|AB|≥$\frac{1}{2}$(a+b).
∴$\frac{|MN|}{|AB|}$≤1,
即 $\frac{|MN|}{|AB|}$的最大值为1.
故答案为:1.
点评 本题给出抛物线的弦AB对焦点F所张的角为直角,求AB中点M到准线的距离与AB比值的取值范围,着重考查了抛物线的定义与简单几何性质、梯形的中位线定理和基本不等式求最值等知识,属于中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.“a≠1或b≠2”是“a+b≠3”的( )
| A. | 必要不充分条件 | B. | 既不充分也不必要条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |
3.设f(x)是定义在R上的奇函数,其图象关于直线x=1对称,且当0<x≤1时,f(x)=log3x.记f(x)在[-10,10]上零点的个数为m,方程f(x)=-1在[-10,10]上的实数根和为n,则有( )
| A. | m=20,n=10 | B. | m=10,n=20 | C. | m=21,n=10 | D. | m=11,n=21 |