题目内容
18.若函数f(x+3)的定义域为[-5,-2],则F(x)=f(x+1)•f(x-1)定义域为( )| A. | [-3,2] | B. | [-7,-6] | C. | [-9,-4] | D. | [-1,0] |
分析 由函数f(x+3)的定义域求出f(x)的定义域,然后再由x+1,x-1
在函数f(x)的定义域内,联立不等式组求解x的取值集合即可.
解答 解:函数f(x+3)的定义域为[-5,-2],即-5≤x≤-2,
则-2≤x+3≤1,∴函数f(x)的定义域为[-2,1],
由$\left\{\begin{array}{l}{-2≤x+1≤1}\\{-2≤x-1≤1}\end{array}\right.$,解得-1≤x≤0.
∴F(x)=f(x+1)+f(x-1)的定义域为[-1,0].
故选:D.
点评 本题考查了函数的定义域及其求法问题,是基础题.
①给出f(x)的定义域为[a,b],f[g(x)]的定义域,就是不等式a≤g(x)≤b得x得取值集合,
②给出f[g(x)]的定义域为[a,b],求解f(x)的定义域,就是在x∈[a,b]内的g(x)的值域.

练习册系列答案
相关题目
8.已知x>0,y>0.则( )
| A. | 若log2x+2x=log2y+3y,则x>y | B. | 若log2x+2x=log2y+3y,则x<y | ||
| C. | 若log2x-2x=log2y-3y,则x>y | D. | 若log2x-2x=log2y-3y,则x<y |
6.直线x+y+1=0关于点(1,2)对称的直线方程为( )
| A. | x+y-7=0 | B. | x-y+7=0 | C. | x+y+6=0 | D. | x-y-6=0 |
3.直线l与抛物线y2=6x交于A,B两点,圆(x-6)2+y2=r2与直线l相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
| A. | ($\sqrt{3}$,2$\sqrt{3}$) | B. | ($\sqrt{3}$,3$\sqrt{3}$) | C. | (3,$2\sqrt{3}$) | D. | (3,3$\sqrt{3}$) |
10.若直线ax-by+1=0(a>0,b>0)分圆C:x2+y2+2x-4y+1=0的周长,则ab的取值范围是( )
| A. | (-∞,$\frac{1}{8}$] | B. | (0,$\frac{1}{8}$] | C. | (0,$\frac{1}{4}$] | D. | [$\frac{1}{4}$,+∞) |
7.已知可导函数f(x)(x∈R)的导数f′(x)满足f′(x)-f(x)<0,则( )
| A. | ef(2015)>f(2016) | B. | ef(2015)<f(2016) | ||
| C. | ef(2015)=f(2016) | D. | ef(2015)与f(2016)的大小不确定 |
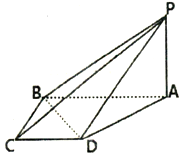 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.