题目内容
3.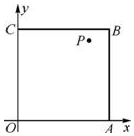 如图,在边长为1的正方形OABC内任取一点P(x,y).
如图,在边长为1的正方形OABC内任取一点P(x,y).(1)求△APB的面积大于$\frac{1}{4}$的概率;
(2)求点P到原点的距离小于1的概率.
分析 (1)根据题意画出图形,结合图形求出满足条件的点P所在的区域面积,利用几何概型计算所求的概率;
(2)符合条件的点P构成的区域是圆x2+y2=1在第一象限所围的平面区域,利用几何概型计算所求的概率.
解答 解:(1)如图所示,取线段BC,AO的中点E,F,连接EF,
则当点P在线段EF上时,S△APB=$\frac{1}{4}$,
∴满足条件的点P所在的区域为矩形OFEC(阴影部分);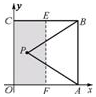
故所求概率为P=$\frac{{S}_{矩形OFEC}}{{S}_{正方形OABC}}$=$\frac{1}{2}$;
(2)所有的点P构成正方形区域D,若点P到原点距离小于1,
则$\left\{\begin{array}{l}{0<x<1}\\{0<y<1}\\{{x}^{2}{+y}^{2}<1}\end{array}\right.$,
所以符合条件的点P构成的区域是
圆x2+y2=1在第一象限所围的平面区域如图中阴影部分,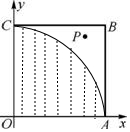
所以点P到原点距离小于1的概率为P=$\frac{\frac{1}{4}•π{•1}^{2}}{{1}^{2}}$=$\frac{π}{4}$.
点评 本题考查了几何概型的计算问题,关键是正确计算出阴影部分的面积,是基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.双曲线4x2-$\frac{y^2}{9}$=1的渐近线方程是( )
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{1}{6}$x | C. | y=±$\frac{3}{2}$x | D. | y=±6x |
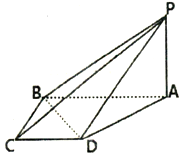 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.