题目内容
已知口袋里有5个红球,15个白球,则从口袋里任取一个球,取到的是红球的概率为 .
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:由题意易得从口袋里任取一个球共20种可能,其中取到的是红球有5种可能,由古典概型可得.
解答:
解:∵袋中共5+15=20个球,
∴从口袋里任取一个球共20种可能,
又∵口袋里有5个红球,
∴从口袋里任取一个球,取到的是红球有5种可能,
∴取到的是红球的概率P=
=
故答案为:
∴从口袋里任取一个球共20种可能,
又∵口袋里有5个红球,
∴从口袋里任取一个球,取到的是红球有5种可能,
∴取到的是红球的概率P=
| 5 |
| 20 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查古典概型,属基础题.

练习册系列答案
相关题目
设O为原点,M(2,-1),若点N(x,y)满足不等式组
,则
•
的最小值是( )
|
| OM |
| ON |
| A、-3 | B、-2 | C、-1 | D、0 |
 一个几何体的三视图是一个正方形,一个矩形,一个半圈,尺寸大小如图所示,则该几何体的表面积是( )
一个几何体的三视图是一个正方形,一个矩形,一个半圈,尺寸大小如图所示,则该几何体的表面积是( )| A、π | B、3π+4 |
| C、π+4 | D、2π+4 |
已知椭圆
+
=1(a>b>0)的左右焦点分别为F1,F2,点P是椭圆上一点,点M是线段PF1的中点,且|OF1|=2|OM|,OM⊥PF1,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设p:f(x)=x3-2x2-mx+1在(-∞,+∞)上单调递增;q:m>
,则p是q的( )
| 4 |
| 3 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、以上都不对 |
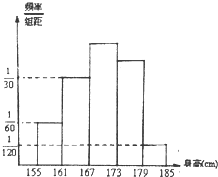 某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )
某校对高三年级男生的身体发育情况进行调查,共抽取60名男生的身高作为样本,其频率分布直方图如图所示,则身高在[167,179)之间的人数为( )