题目内容
10．函数y=1-2sin2（x+$\frac{π}{4}$）是（ ）| A． | 以2π为周期的偶函数 | B． | 以π为周期的偶函数 | ||
| C． | 以2π为周期的奇函数 | D． | 以π为周期的奇函数 |
分析 直接由二倍角的余弦和诱导公式可得y=-sin2x，可判周期性和奇偶性．
解答 解：函数f（x）=1-2sin2（x+$\frac{π}{4}$）=cos2（x+$\frac{π}{4}$）=cos（2x+$\frac{π}{2}$）=-sin2x，
∴函数y=1-2sin2（x+$\frac{π}{4}$）是以π为周期的奇函数．
故选：D．
点评 本题主要考查二倍角公式的应用，正弦函数的周期性和奇偶性，属于基础题．
练习册系列答案
相关题目
20．i为虚数单位，复数$\frac{2i}{1-i}$在复平面内对应的点到原点的距离为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\sqrt{2}$ | D． | 1 |
1．函数y=f（x）是定义域为R的偶函数，当x≥0时，f（x）=$\left\{\begin{array}{l}{\frac{1}{16}{x}^{2}（0≤x≤2）}\\{（\frac{1}{2}）^{x}（x＞2）}\end{array}\right.$，若关于x的方程[f（x）]2+af（x）+b=0，a，b∈R有且仅有5个不同实数根，则实数a的取值范围是（ ）
| A． | （-$\frac{1}{4}$，0） | B． | （$-\frac{1}{2}$，-$\frac{1}{4}$） | C． | （$-\frac{1}{2}$，$-\frac{1}{4}$）∪（$-\frac{1}{4}$，-$\frac{1}{8}$） | D． | （-$\frac{1}{2}$，$-\frac{1}{8}$） |
18．[x]表示不超过x的最大整数，例如[1.7]=1，[-3.1]=-4，已知f（x）=x-[x]（x∈R），g（x）=lg|x|，则函数h（x）=f（x）-g（x）的零点个数是（ ）
| A． | 15 | B． | 16 | C． | 17 | D． | 18 |
5．
某校高三年级在学期末进行的质量检测中，考生数学成绩情况如下表所示：
已知用分层抽样方法在不低于135分的考生中随机抽取5名考生进行质量分析，其中文科考生抽取了1名．
（1）求z的值；
（2）如图是文科不低于135分的6名学生的数学成绩的茎叶图，计算这6名考生的数学成绩的方差；
（3）已知该校数学成绩不低于120分的文科理科考生人数之比为1：3，不低于105分的文科理科考生人数之比为2：5，求理科数学及格人数．
某校高三年级在学期末进行的质量检测中，考生数学成绩情况如下表所示：| 数学成绩 | [90，105） | [105，120） | [120，135） | [135，150] |
| 文科考生 | 57 | 40 | 24 | 6 |
| 理科考生 | 123 | x | y | z |
（1）求z的值；
（2）如图是文科不低于135分的6名学生的数学成绩的茎叶图，计算这6名考生的数学成绩的方差；
（3）已知该校数学成绩不低于120分的文科理科考生人数之比为1：3，不低于105分的文科理科考生人数之比为2：5，求理科数学及格人数．
15．函数f（x）=lg（$\frac{2}{1-x}$+a）是奇函数，则a的值为（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | 不存在 |
2．函数y=log3（x2-2x+4）的值域为（ ）
| A． | [1，+∞） | B． | [0，+∞） | C． | [3，+∞） | D． | R |
19．
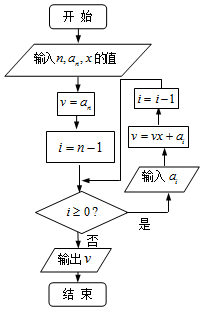如图程序框图的算法思路，源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法，执行该程序框图，若输入的n，an，x分别为5，1，-2，且a4=5，a3=10，a2=10，a1=5，a0=1，则输出的v=（ ）
如图程序框图的算法思路，源于我国南宋时期的数学家秦九韶在他的著作《数书九章》中提出的秦九韶算法，执行该程序框图，若输入的n，an，x分别为5，1，-2，且a4=5，a3=10，a2=10，a1=5，a0=1，则输出的v=（ ）| A． | 1 | B． | 2 | C． | -1 | D． | -2 |
20．若曲线x2+y2+a2x+（1-a2）y-4=0关于直线y=x对称的曲线仍是其本身，则实数a为（ ）
| A． | $\frac{1}{2}$或$-\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$或$-\frac{{\sqrt{2}}}{2}$ | C． | $\frac{1}{2}$或$-\frac{{\sqrt{2}}}{2}$ | D． | $-\frac{1}{2}$或$\frac{{\sqrt{2}}}{2}$ |