题目内容

18．[x]表示不超过x的最大整数，例如[1.7]=1，[-3.1]=-4，已知f（x）=x-[x]（x∈R），g（x）=lg|x|，则函数h（x）=f（x）-g（x）的零点个数是（　　）
A．15B．16C．17D．18

分析 作函数f（x）=x-[x]（x∈R）与g（x）=log2015x的图象，从而化函数h（x）=f（x）-g（x）的零点个数为图象的交点的个数．

解答 解：作函数f（x）=x-[x]（x∈R）与g（x）=lg|x|的图象如下，lg10=1，lg|-10|=1
由图象可知：
函数f（x）与g（x）的图象在每个区间[n，n+1]（1≤n＜10）都有一个交点，
故函数f（x）与g（x）的图象共有2×9=18，
故选：D．

点评 本题考查了函数的图象的作法与应用．函数的零点个数的求法，考查数形结合以及计算能力．

练习册系列答案
相关题目
8．在△ABC中，内角A，B，C所对应的边分别为a，b，c，且$\frac{c}{b}=\sqrt{2}sinC$．
（1）求B；
（2）若a=6，△ABC的面积为9，求b的长，并判断△ABC的形状．
9．在正棱柱ABC-A1B1C1中，D是AC的中点，AA1：AB=$\sqrt{2}$：1，则异面直线AB1与BD所成的角为（　　）
A．30°B．45°C．60°D．90°
6．记△ABC的三个内角分别为A，B，C，设$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为θ，已知$\overrightarrow{AB}$$•\overrightarrow{BC}$=6，且6（2-$\sqrt{3}$）≤|$\overrightarrow{AB}$||$\overrightarrow{BC}$|sin（π-θ）≤6$\sqrt{3}$．
（Ⅰ）求tan15°的值和角θ的取值范围；
（Ⅱ）求函数f（θ）=$\frac{1-\sqrt{2}cos（2θ-\frac{π}{4}）}{sinθ}$的最大值．
13．函数y=f（x）的图象向右平移$\frac{π}{3}$单位后与函数y=cos2x的图象重合，则y=f（x）的解析式是（　　）
A．f（x）=cos（2x$+\frac{π}{3}$）B．f（x）=-cos（2x-$\frac{π}{6}$）C．f（x）=-sin（2x+$\frac{π}{6}$）D．f（x）=sin（2x-$\frac{π}{6}$）
3．已知{an}，{bn}为两个数列，其中{an}是等差数列且前n项和为Sn又a3=6，a9=18．
（1）求数列{an}的通项公式；
（2）若数列{bn}满足a1b1+a2b2+…+anbn=（2n-3）Sn，求数列{bn}的通项公式．
10．函数y=1-2sin2（x+$\frac{π}{4}$）是（　　）
A．以2π为周期的偶函数B．以π为周期的偶函数
C．以2π为周期的奇函数D．以π为周期的奇函数
7．函数f（x）=Asin（ωx+φ），x∈R（0，ω＞0，0＜φ＜$\frac{π}{2}$）的图象与x轴的交点中，相邻两个交点之间的距离为$\frac{π}{2}$，且图象上一个最低点为M（$\frac{2π}{3}$，-2）．
（1）求函数f（x）的解析式及单调增区间；
（2）求 当x∈[$\frac{π}{12}$，$\frac{π}{2}$]时，f（x）的值域．
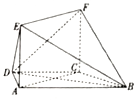8．如图，在梯形ABCD中，AB∥CD，AD=DC=CB=a，∠ABC=60°，平面ACFE⊥平面ABCD，四边形ACFE是矩形．
（1）求证：BC⊥平面ACFE；
（2）若AD=AE，求平面BDF与平面ACFE所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网