题目内容
20.i为虚数单位,复数$\frac{2i}{1-i}$在复平面内对应的点到原点的距离为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
分析 由复数代数形式的乘除运算化简复数$\frac{2i}{1-i}$,求出在复平面内对应的点的坐标,则答案可求.
解答 解:$\frac{2i}{1-i}$=$\frac{2i(1+i)}{(1-i)(1+i)}=-1+i$,
复数$\frac{2i}{1-i}$在复平面内对应的点的坐标为:(-1,1),到原点的距离为:$\sqrt{2}$.
故选:C.
点评 本题考查了复数代数形式的乘除运算,考查了复数的代数表示法及其几何意义,是基础题.

练习册系列答案
相关题目
9.在正棱柱ABC-A1B1C1中,D是AC的中点,AA1:AB=$\sqrt{2}$:1,则异面直线AB1与BD所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.函数y=1-2sin2(x+$\frac{π}{4}$)是( )
| A. | 以2π为周期的偶函数 | B. | 以π为周期的偶函数 | ||
| C. | 以2π为周期的奇函数 | D. | 以π为周期的奇函数 |
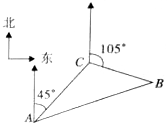 如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.
如图,某船在海上航行中遇险发出呼救信号,我海上救生艇在A处获悉后,立即测出该船在方位角45°方向,相距10海里的C处,还测得该船正沿方位角105°的方向以每小时9海里的速度行驶,救生艇立即以每小时21海里的速度前往营救,则救生艇与呼救艇与呼救船在B处相遇所需的最短时间为$\frac{2}{3}$小时.