题目内容
某四面体的三视图如图所示,三个三角形均为直角三角形,则该四面体的表面积是( )
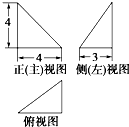

| A、8 | ||
B、22+2
| ||
C、18+6
| ||
D、24+6
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据几何体的三视图,得出该几何体是三棱锥,并根据三棱锥的各棱之间的关系,求出它的表面积.
解答:
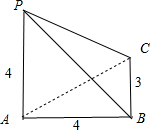 解:根据几何体的三视图知,
解:根据几何体的三视图知,
该几何体是三棱锥,如图所示;
且底面△ABC为俯视图中的直角三角形,∠ABC=90°,
其中AB=4,BC=3,∴AC=5,
PA⊥底面ABC,且PA=4,
∴∠PAB=∠PAC=90°,CB⊥PB;
∴S△ABC=
AB•BC=
×4×3=6,
S△PAB=
PA•AB=
×4×4=8,
S△PAC=
PA•AC=
×4×5=10,
S△PBC=
PB•BC=
×
×3=6
;
∴三棱锥P-ABC的表面积为
S=S△ABC+S△PAB+S△PAC+S△PBC=6+8+10+6
=24+6
.
故选:D.
 解:根据几何体的三视图知,
解:根据几何体的三视图知,该几何体是三棱锥,如图所示;
且底面△ABC为俯视图中的直角三角形,∠ABC=90°,
其中AB=4,BC=3,∴AC=5,
PA⊥底面ABC,且PA=4,
∴∠PAB=∠PAC=90°,CB⊥PB;
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 42+42 |
| 2 |
∴三棱锥P-ABC的表面积为
S=S△ABC+S△PAB+S△PAC+S△PBC=6+8+10+6
| 2 |
| 2 |
故选:D.
点评:本题考查了空间几何体的三视图的应用问题,解题时应根据三视图得出该几何体的结构特征,是基础题.

练习册系列答案
相关题目
设f(n)>0(n∈N*),f(2)=4,并且对于任意n2,n2∈N*,有f(n1+n2)=f(n1)•f(n2)成立,猜想f(n)的表达式为( )
| A、f(n)=n2 |
| B、f(n)=2n |
| C、f(n)=2n+1 |
| D、f(n)=2n |
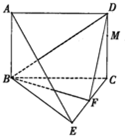 如图,平面ABCD⊥平面BCE,四边形ABCD为矩形,BC=CE,点F为CE的中点.
如图,平面ABCD⊥平面BCE,四边形ABCD为矩形,BC=CE,点F为CE的中点.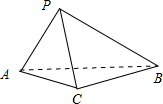 如图,已知四面体PABC的四个顶点P,A,B,C均在球O的表面上,且AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,则球O的体积是
如图,已知四面体PABC的四个顶点P,A,B,C均在球O的表面上,且AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC,则球O的体积是