题目内容
已知函数f(x)=
(sin2x-cos2x)-2sinxcosx
(1)求f(x)的最小正周期;
(2)设x∈[-
,
],求f(x)的值域和单调递增区间.
| 3 |
(1)求f(x)的最小正周期;
(2)设x∈[-
| π |
| 2 |
| π |
| 2 |
考点:三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)首先,化简函数解析式,然后,借助于周期公式进行求解;
(2)结合给定的x∈[-
,
],求解其值域和单调递增区间.
(2)结合给定的x∈[-
| π |
| 2 |
| π |
| 2 |
解答:
解:(1)∵函数f(x)=
(sin2x-cos2x)-2sinxcosx
=-
cos2x-sin2x
=-sin(2x+
),
∴f(x)=-sin(2x+
),
∴T=
=π,
∴f(x)的最小正周期π;
(2)∵x∈[-
,
],
∴2x∈[-π,π],
∴(2x+
)∈[-
,
],
∴sin(2x+
)∈[-1,1],
∴-sin(2x+
)∈[-1,1],
∴f(x)的值域[-1,1],
令-
+2kπ≤2x+
≤
+2kπ,k∈Z,
∴-
+2kπ≤2x≤
+2kπ,
∴-
+kπ≤x≤
+kπ,
∵x∈[-
,
],
∴该函数的单调递增区间为[0,
].
| 3 |
=-
| 3 |
=-sin(2x+
| π |
| 3 |
∴f(x)=-sin(2x+
| π |
| 3 |
∴T=
| 2π |
| 2 |
∴f(x)的最小正周期π;
(2)∵x∈[-
| π |
| 2 |
| π |
| 2 |
∴2x∈[-π,π],
∴(2x+
| π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
∴sin(2x+
| π |
| 3 |
∴-sin(2x+
| π |
| 3 |
∴f(x)的值域[-1,1],
令-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
∴-
| 5π |
| 6 |
| π |
| 6 |
∴-
| 5π |
| 12 |
| π |
| 12 |
∵x∈[-
| π |
| 2 |
| π |
| 2 |
∴该函数的单调递增区间为[0,
| π |
| 12 |
点评:本题重点考查了三角公式、三角恒等变换公式、三角函数的图象与性质等知识,属于中档题.

练习册系列答案
相关题目
设f(n)>0(n∈N*),f(2)=4,并且对于任意n2,n2∈N*,有f(n1+n2)=f(n1)•f(n2)成立,猜想f(n)的表达式为( )
| A、f(n)=n2 |
| B、f(n)=2n |
| C、f(n)=2n+1 |
| D、f(n)=2n |
向量
=(1,m),
=(2,-4),若
=λ
(λ为实数),则m的值为( )
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
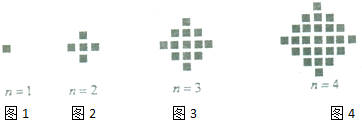 图为某少数民族最常见的四个刺绣图案,这些图案都是小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
图为某少数民族最常见的四个刺绣图案,这些图案都是小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.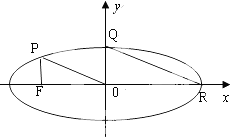 过椭圆
过椭圆