题目内容
计算：tan70°•cos10°•（1-
tan20°）= ．
| 3 |
考点：三角函数的恒等变换及化简求值
专题：三角函数的求值
分析：首先，将题目中的正切化为正弦与余弦的比，然后，通分并结合辅助角公式进行化简即可．
解答：
解：tan70°•cos10°•（1-
tan20°）
=
•cos10°•
=
•cos10°•2
=
=1．
故答案为：1．
| 3 |
=
| sin70° |
| cos70° |
cos20°-
| ||
| cos20° |
=
| cos20° |
| sin20° |
| sin(30°-20°) |
| cos20° |
=
| cos20°•2sin10°cos10° |
| sin20°cos20° |
=1．
故答案为：1．
点评：本题重点考查了三角恒等变换公式、三角公式、同角三角函数基本关系式等知识，属于中档题．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
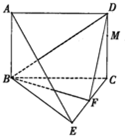如图，平面ABCD⊥平面BCE，四边形ABCD为矩形，BC=CE，点F为CE的中点．已知向量
=（3，-2），
=（-2，1），
=（7，-4），试用
和
来表示
，下面正确的表述是（ ）
| a |
| b |
| c |
| a |
| b |
| c |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
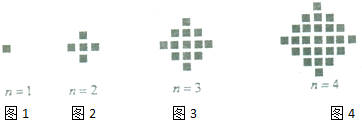图为某少数民族最常见的四个刺绣图案，这些图案都是小正方形构成，小正方形数越多刺绣越漂亮，现按同样的规律刺绣（小正方形的摆放规律相同），设第n个图形包含f（n）个小正方形．
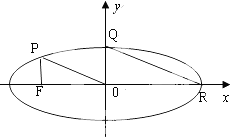过椭圆