题目内容
| 1-sin2100° |
| A、cos100° |
| B、±cos100° |
| C、±cos80° |
| D、cos80° |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：原式利用二次根式的化简公式变形，再利用绝对值的代数意义化简即可得到结果．
解答：
解：∵cos100°=cos（90°+10°）=-sin10°＜0，即sin10°＞0，
∴原式=|cos100°|=|cos（90°+10°）|=|-sin10°|=cos80°，
故选：D．
∴原式=|cos100°|=|cos（90°+10°）|=|-sin10°|=cos80°，
故选：D．
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
已知f（x）=xln x，若f′（x0）=2，则x0等于（ ）
| A、e2 | ||
| B、e | ||
C、
| ||
| D、ln 2 |
已知函数f（x）的导函数为f′（x），且满足f（x）=2xf′（
）+cosx，则f′（
）的值为（ ）
| π |
| 2 |
| π |
| 4 |
A、2+
| ||||
B、2-
| ||||
C、
| ||||
D、-
|
设m，n是两条不同的直线，α，β是两个不同的平面．（ ）
| A、若m∥α，n?α，则m∥n |
| B、若m⊥α，n?α，则m⊥n |
| C、若α∥β，m?α，n?β，则m∥n |
| D、若α⊥β，m?α，n?β，则m⊥n |
已知f′（x）是函数f（x）=x3-x+1的导数，则
的值是（ ）
| f′(1) |
| f(1) |
| A、0 | B、1 | C、2 | D、3 |
函数y=cosx•ln|x|的部分图象大致是下图中的（ ）
A、 |
B、 |
C、 |
D、 |
三次函数f（x）=ax3+2x+5在x∈（-∞，+∞）内是增函数，则（ ）
| A、a＞0 | ||
| B、a＜0 | ||
| C、a=1 | ||
D、a=
|
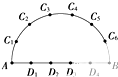如图，在以AB为直径的半圆周上，有异于A、B的六个点C1、C2、C3、C4、C5、C6，直径AB上有异于A、B的四个点D1、D2、D3、D4．以这10个点中的3个点为顶点作三角形可作出多少个（ ）