题目内容
18.在△ABC中,点O在线段BC的延长线上,且|$\overrightarrow{BO}$|=3|$\overrightarrow{CO}$|,当$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$时,x-y=( )| A. | -2 | B. | -2 | C. | 2 | D. | 3 |
分析 可作出图形,然后由条件便可得到$\overrightarrow{BO}=\frac{3}{2}\overrightarrow{BC}=\frac{3}{2}(\overrightarrow{AC}-\overrightarrow{AB})$,根据向量加法的几何意义及向量的数乘运算便可得到$\overrightarrow{AO}=-\frac{1}{2}\overrightarrow{AB}+\frac{3}{2}\overrightarrow{AC}$,从而由平面向量基本定理即可得出x,y的值,从而求出x-y的值.
解答 解:如图,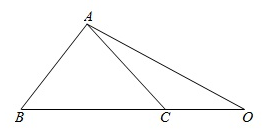
根据条件,$\overrightarrow{BO}=3\overrightarrow{CO}$;
∴$\overrightarrow{BO}=\frac{3}{2}\overrightarrow{BC}=\frac{3}{2}(\overrightarrow{AC}-\overrightarrow{AB})$;
∴$\overrightarrow{AO}=\overrightarrow{AB}+\overrightarrow{BO}$=$\overrightarrow{AB}+\frac{3}{2}(\overrightarrow{AC}-\overrightarrow{AB})=-\frac{1}{2}\overrightarrow{AB}+\frac{3}{2}\overrightarrow{AC}$;
又$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$;
∴$x=-\frac{1}{2},y=\frac{3}{2}$;
∴x-y=-2.
故选:A.
点评 考查向量加法、减法及数乘的几何意义,以及向量的数乘运算,平面向量基本定理.

 名校课堂系列答案
名校课堂系列答案| A. | 2 | B. | -2 | C. | -1 | D. | 1 |
 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=BC=CC1=2CD,E为线段AB的中点,F是线段DD1上的动点.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=BC=CC1=2CD,E为线段AB的中点,F是线段DD1上的动点.