题目内容
8. 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=BC=CC1=2CD,E为线段AB的中点,F是线段DD1上的动点.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB=BC=CC1=2CD,E为线段AB的中点,F是线段DD1上的动点.(Ⅰ)求证:EF∥平面BCC1B1;
(Ⅱ)若∠BCD=∠C1CD=60°,且平面D1C1CD⊥平面ABCD,求平面BCC1B1与DC1B1平面所成的角(锐角)的余弦值.
分析 (I)连结DE,D1E,则可证明平面DED1∥平面BCC1B1,故而EF∥平面BCC1B1.
(II)过D作DH⊥BC,利用勾股定理可得BD⊥CD,C1D⊥CD,故C1D⊥平面ABCD,于是B1C1⊥C1D,由BC⊥平面C1DH可得B1C1⊥C1H,于是∠DC1H为平面BCC1B1与DC1B1平面所成的角.使用平面几何知识求出C1D和C1H,得出∠DC1H的余弦值.
解答 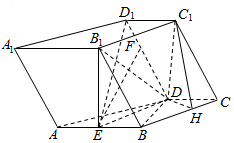 证明:(I)连结DE,D1E,∵AB∥CD,AB=2CD,E是AB的中点,
证明:(I)连结DE,D1E,∵AB∥CD,AB=2CD,E是AB的中点,
∴BE∥CD,BE=CD,
∴四边形BCDE是平行四边形,
∴DE∥BC,又DE?平面BCC1B1,BC?平面BCC1B1,
∴DE∥平面BCC1B1,
∵D1D∥C1C,D1D?平面BCC1B1,C1C?平面BCC1B1,
∴D1D∥平面BCC1B1,
又D1D?平面DED1,DE?平面DED1,D1D∩DE=D,
∴平面DED1∥平面BCC1B1,
∵EF?平面DED1,
∴EF∥平面BCC1B1.
(II)∵AB=BC=CC1=2CD,∠BCD=∠C1CD=60°,
设CD=1,则BC=2,
在△BCD中,由余弦定理得BD2=BC2+CD2-2BC•CD•cos∠BCD=3,
∴BC2=CD2+BD2,
∴BD⊥CD.
同理:C1D⊥CD,
∵平面D1C1CD⊥平面ABCD,平面D1C1CD∩平面ABCD=CD,C1D?平面D1C1CD,
∴C1D⊥平面ABCD,∵BC?平面ABCD,
∴C1D⊥BC.
在平面ABCD中,过D作DH⊥BC,垂足为H,连结C1H.
∵DH?平面C1DH,C1D?平面C1DH,DH∩C1D=D,
∴BC⊥平面C1DH,∵C1H?平面C1DH,
∴BC⊥C1H,
∵BC∥B1C1,
∴C1D⊥B1C1,B1C1⊥C1H,
又C1D?平面DC1B1,C1H?平面BCC1B1,
∴∠DC1H为平面BCC1B1与DC1B1平面所成的角.
在Rt△BCD中,DH=$\frac{BD•CD}{BC}=\frac{\sqrt{3}}{2}$,又C1D=$\sqrt{3}$,
∴在Rt△C1DH,C1H=$\sqrt{{C}_{1}{D}^{2}+D{H}^{2}}$=$\frac{\sqrt{15}}{2}$,
∴cos∠DC1H=$\frac{{C}_{1}D}{{C}_{1}H}$=$\frac{2\sqrt{5}}{5}$.
∴平面BCC1B1与DC1B1平面所成的角(锐角)的余弦值为$\frac{2\sqrt{5}}{5}$.
点评 本题考查了线面平行的判定定理,二面角的求法,构造平行平面和作出二面角是解题关键,属于难题.

| A. | 1 | B. | -1 | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
| A. | (-$\frac{π}{4}$,0) | B. | (0,0) | C. | ($\frac{θ}{2}$,0) | D. | (θ,0) |
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | 5 | D. | 4 |

| A. | 4 | B. | 6 | C. | 18 | D. | 24 |