题目内容

6．给定min{a，b}=$\left\{\begin{array}{l}{a，a≤b}\\{b，b＜a}\end{array}\right.$，已知函数f（x）=min{x，x2-4x+4}+4，若动直线y=m与函数y=f（x）的图象有3个交点，它们的横坐标分别为x1，x2，x3，则x1+x2+x3的范围为（4，5）．

分析 画出函数f（x）的图象以及直线y=k的图象，根据条件数形结合求得k的范围．

解答 解：设g（x）=min{x，x2-4x+4}，则f（x）=g（x）+4，
故把g（x）的图象向上平移4各单位，
可得f（x）的图象，
函数f（x）=min{x，x2-4x+4}+4的图象如图所示：
由于直线y=m与函数y=f（x）的图象有3个交点，
数形结合可得k的范围为（4，5）．
故答案为：（4，5）．

点评 本题考查函数与方程的综合运用，以及数形结合思想，综合运用知识分析解决新问题的能力，属于中档题．

练习册系列答案
相关题目
16．在△ABC中，角A，B，C所对的边分别为a，b，c，若△ABC的面积S=$\frac{1}{2}$bc，且a=5．
（1）求△ABC的面积的最大值，并判断此时△ABC的形状；
（2）若tanB=$\frac{3}{4}$，$\overrightarrow{CB}$=λ$\overrightarrow{CD}$（λ＞0），|$\overrightarrow{AD}$|=$\frac{4\sqrt{10}}{5}$，求λ的值．
17．已知函数f（x）=（1-$\frac{a}{x}$）ex（x＞0），其中e为自然对数的底数．当a=2时，则曲线y=f（x）在（1，f（1））处的切线与坐标轴围成的面积为（　　）
A．eB．2eC．3eD．4e
14．已知函数f（x）的定义域为实数集R，$?x∈R，f（{x-90}）=\left\{\begin{array}{l}lgx，x＞0\\-x，x≤0\end{array}\right.$，则f（10）-f（-100）的值为（　　）
A．-8B．-16C．55D．101
1．在△ABC中，D为线段BC上一点，且$BD=\frac{1}{5}BC$，以向量$\overrightarrow{AB}，\overrightarrow{AC}$作为一组基底，则$\overrightarrow{AD}$等于（　　）
A．$\frac{1}{5}\overrightarrow{AB}+\frac{4}{5}\overrightarrow{AC}$B．$\frac{2}{5}\overrightarrow{AB}+\frac{3}{5}\overrightarrow{AC}$C．$\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}$D．$\frac{4}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$
11．执行如图所示的程序框图，若输出的$S=\frac{25}{24}$，则判断框内填入的条件可以是（　　）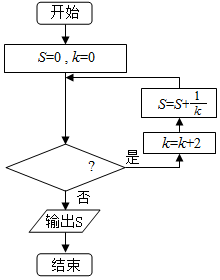
A．k≥7B．k＞7C．k≤8D．k＜8
18．在△ABC中，点O在线段BC的延长线上，且|$\overrightarrow{BO}$|=3|$\overrightarrow{CO}$|，当$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$时，x-y=（　　）
A．-2B．-2C．2D．3
15．已知正项数列{an}的前n项和为Sn，且满足Sn=2an-$\frac{1}{2}$．
（1）证明；数列{an}是等比数列；
（2）设bn=log2a2n+1，求数列{$\frac{1}{{b}_{n}{b}_{n+1}}$}的前n项和Tn．
16．在△ABC中，设$\overrightarrow{CB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$且|$\overrightarrow{a}$|=2，|$\overrightarrow{b}$|=$\sqrt{3}$，$\overrightarrow{a}•\overrightarrow{b}$=-$\sqrt{3}$，求AB．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网