题目内容
11.同时具有性质“①最小正周期是4π;②$x=\frac{π}{3}$是图象的一条对称轴;③在区间$(\frac{2π}{3},\frac{5π}{6})$上是减函数”的一个函数是( )| A. | $y=sin(2x-\frac{π}{6})$ | B. | $y=cos(2x-\frac{π}{6})$ | C. | $y=cos(\frac{x}{2}+\frac{π}{3})$ | D. | $y=sin(\frac{x}{2}+\frac{π}{3})$ |
分析 利用函数的周期,求出ω,利用图象关系直线x=$\frac{π}{3}$对称,即可判断选项的正误.
解答 解:对于选项A、B,∵T=$\frac{2π}{2}$=π,故A,B不正确;
对于选项C,如果x=$\frac{π}{3}$为对称轴.
所以$\frac{\frac{π}{3}}{2}$+$\frac{π}{3}$=kπ,k∈Z,可得$\frac{π}{2}$=kπ,k不存在,不满足题意,故C不正确;
对于选项D,因为T=$\frac{2π}{\frac{1}{2}}$=4π,且由$\frac{x}{2}+\frac{π}{3}$=k$π+\frac{π}{2}$,k∈Z,解得图象的对称轴方程为:x=2kπ+$\frac{π}{3}$,k∈Z,当k=0时,x=$\frac{π}{3}$为图象的一条对称轴.
由2kπ$+\frac{π}{2}$≤$\frac{x}{2}+\frac{π}{3}$≤2kπ$+\frac{3π}{2}$,k∈Z,解得单调递减区间为:[4kπ+$\frac{π}{3}$,4kπ+$\frac{7π}{3}$],k∈Z,可得函数在区间$(\frac{2π}{3},\frac{5π}{6})$上是减函数,故D正确.
故选:D.
点评 本题考查三角函数的周期性及其求法,正弦函数的对称性和单调性,考查推理能力,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
1.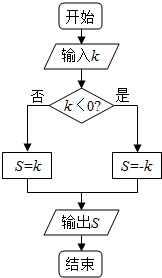 直线l斜率为$\frac{1}{2}$,倾斜角为α,将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )
直线l斜率为$\frac{1}{2}$,倾斜角为α,将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )
 直线l斜率为$\frac{1}{2}$,倾斜角为α,将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )
直线l斜率为$\frac{1}{2}$,倾斜角为α,将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
2.下列算法的理解不正确的是( )
| A. | 算法需要一步步执行,且每一步都能得到唯一的结果 | |
| B. | 算法的一个共同特点是对一类问题都有效而不是个别问题 | |
| C. | 任何问题都可以用算法来解决 | |
| D. | 算法一般是机械的,有时要进行大量重复的计算,它的优点是一种通法 |
6.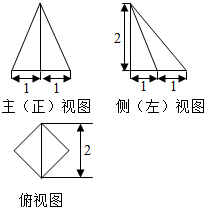 已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据.那么该棱锥的表面积是( )
已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据.那么该棱锥的表面积是( )
 已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据.那么该棱锥的表面积是( )
已知某棱锥的三视图如图所示,俯视图为正方形,根据图中所给的数据.那么该棱锥的表面积是( )| A. | 8+4$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 2$\sqrt{2}$+2$\sqrt{3}$ | D. | 2+2$\sqrt{2}$+2$\sqrt{3}$ |