题目内容
2.下列算法的理解不正确的是( )| A. | 算法需要一步步执行,且每一步都能得到唯一的结果 | |
| B. | 算法的一个共同特点是对一类问题都有效而不是个别问题 | |
| C. | 任何问题都可以用算法来解决 | |
| D. | 算法一般是机械的,有时要进行大量重复的计算,它的优点是一种通法 |
分析 直接由算法的特性可判断四个选项中说法的正误即可得出正确答案.
解答 解:A,由算法的有序性及明确性可知:算法从初始步骤开始,分为若干明确的步骤,每一步都只能有一个确定的继任者,只有执行完前一步才能进入到后一步,并且每一步都确定无误后,才能解决问题,且算法中的每一个步骤都是确切的,能有效地执行且得到确定的结果,不能模棱两可.故A正确;
B,由算法的普遍性:写出的算法必须能解决一类问题,并且能重复使用,这是设计算法的一条基本原则,这样才能使算法更有价值,故正确;
C,算法通常是指用计算机按照一定规则解决一类问题的明确和有限的步骤,并不是任何问题都可以用算法来解决,故不正确;
D,算法一般是机械的,有时要进行大量重复的计算,算法必须能解决一类问题,是一种通法,故正确.
故选:C.
点评 本题考查了命题的真假判断与应用,考查了算法的特性,是基础题.

练习册系列答案
相关题目
13.设集合A={x|x2-2x≥0},集合B={x|2x>1},则A∩B=( )
| A. | (0,2] | B. | [0,2] | C. | [2,+∞) | D. | (2,+∞) |
14.执行如图所示的程序框图,若m=3,则输出的结果为( )
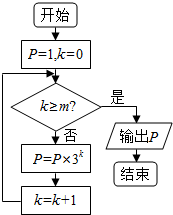

| A. | 3 | B. | 27 | C. | 81 | D. | 729 |
11.同时具有性质“①最小正周期是4π;②$x=\frac{π}{3}$是图象的一条对称轴;③在区间$(\frac{2π}{3},\frac{5π}{6})$上是减函数”的一个函数是( )
| A. | $y=sin(2x-\frac{π}{6})$ | B. | $y=cos(2x-\frac{π}{6})$ | C. | $y=cos(\frac{x}{2}+\frac{π}{3})$ | D. | $y=sin(\frac{x}{2}+\frac{π}{3})$ |
