题目内容
3.在平面直角坐标系xOy中,已知直线l:x+y+m=0和圆M:x2+y2=9,若圆M上存在点P,使得P到直线l的距离为2,则实数m的取值范围是[-5$\sqrt{2}$,5$\sqrt{2}$].分析 设P(3cosθ,3sinθ),0≤θ<2π,求出P到直线l的距离,利用三铁函数的性质能求出实数m的取值范围.
解答 解:∵直线l:x+y+m=0和圆M:x2+y2=9,若圆M上存在点P,使得P到直线l的距离为2,
∴设P(3cosθ,3sinθ),0≤θ<2π,
∴P到直线l的距离d=$\frac{|3cosθ+3sinθ+m|}{\sqrt{2}}$=$\frac{|3\sqrt{2}sin(θ+\frac{π}{4})+m|}{\sqrt{2}}$=2,
∵-3$\sqrt{2}$$≤3\sqrt{2}sin(θ+\frac{π}{4})$$≤3\sqrt{2}$,|3$\sqrt{2}sin(θ+\frac{π}{4})$+m|=2$\sqrt{2}$,
∴-5$\sqrt{2}≤m≤5\sqrt{2}$,
∴实数m的取值范围是[-5$\sqrt{2}$,5$\sqrt{2}$].
故答案为:[-5$\sqrt{2}$,5$\sqrt{2}$].
点评 本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
13.设集合A={x|x2-2x≥0},集合B={x|2x>1},则A∩B=( )
| A. | (0,2] | B. | [0,2] | C. | [2,+∞) | D. | (2,+∞) |
14.执行如图所示的程序框图,若m=3,则输出的结果为( )
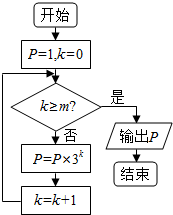

| A. | 3 | B. | 27 | C. | 81 | D. | 729 |
11.同时具有性质“①最小正周期是4π;②$x=\frac{π}{3}$是图象的一条对称轴;③在区间$(\frac{2π}{3},\frac{5π}{6})$上是减函数”的一个函数是( )
| A. | $y=sin(2x-\frac{π}{6})$ | B. | $y=cos(2x-\frac{π}{6})$ | C. | $y=cos(\frac{x}{2}+\frac{π}{3})$ | D. | $y=sin(\frac{x}{2}+\frac{π}{3})$ |
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,-1),离心率e=$\frac{\sqrt{6}}{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,-1),离心率e=$\frac{\sqrt{6}}{3}$.