题目内容
1.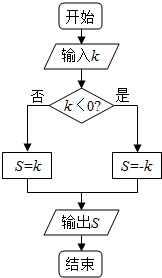 直线l斜率为$\frac{1}{2}$,倾斜角为α,将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )
直线l斜率为$\frac{1}{2}$,倾斜角为α,将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k,则将k值执行如图所示程序后,输出S值为( )| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
分析 由已知利用二倍角的正切函数公式求得旋转后的直线的斜率,执行程序框图,可得k=$\frac{4}{3}$时,不满足条件k<0,S=$\frac{4}{3}$.
解答 解:∵直线l的斜率是$\frac{1}{2}$,倾斜角为α,
∴tan$α=\frac{1}{2}$,
∵将l绕它与x轴的交点逆时针方向旋转α后所得直线的斜率为k,
∴k=tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×\frac{1}{2}}{1-(\frac{1}{2})^{2}}$=$\frac{4}{3}$,
∴执行程序框图,可得k=$\frac{4}{3}$时,不满足条件k<0,S=k=$\frac{4}{3}$.
故选:A.
点评 本题考查直线的斜率与直线的倾斜角的关系,注意直线的旋转的方向,角的正负,考查计算能力及程序框图,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.执行如图所示的程序框图,如果输入的x,t均为2,则输出的M等于( )
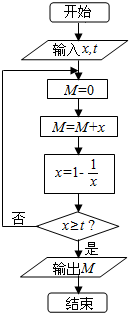

| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{7}{2}$ |
13.设集合A={x|x2-2x≥0},集合B={x|2x>1},则A∩B=( )
| A. | (0,2] | B. | [0,2] | C. | [2,+∞) | D. | (2,+∞) |
11.同时具有性质“①最小正周期是4π;②$x=\frac{π}{3}$是图象的一条对称轴;③在区间$(\frac{2π}{3},\frac{5π}{6})$上是减函数”的一个函数是( )
| A. | $y=sin(2x-\frac{π}{6})$ | B. | $y=cos(2x-\frac{π}{6})$ | C. | $y=cos(\frac{x}{2}+\frac{π}{3})$ | D. | $y=sin(\frac{x}{2}+\frac{π}{3})$ |
