题目内容
已知函数f(x)=ex-1,g(x)=-x2+4x-4.若有f(a)=g(b),则b的取值范围为( )
A、[2-
| ||||
B、(2-
| ||||
| C、[1,3] | ||||
| D、(1,3) |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:先求出f(x)的取值范围,从而得到不等式,解出即可.
解答:
解:∵f(x)=ex-1>-1,
∴-x2+4x-4>-1,
∴x2-4x+3<0,
解得:1<x<3,
故选:D.
∴-x2+4x-4>-1,
∴x2-4x+3<0,
解得:1<x<3,
故选:D.
点评:本题考查了函数的零点问题,考查了转化思想,是一道基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
若F(
)=x,则下列等式正确的是( )
| 1-x |
| 1+x |
| A、F(2-x)=1-F(x) | ||
B、F(-x)=
| ||
| C、F(x-1)=F(x) | ||
| D、F(F(x))=-x |
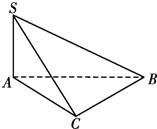 已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.
已知△ABC中,∠BAC=90°,SA⊥面ABC,且SA=3,AB=AC=4.