题目内容

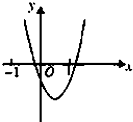二次函数y=ax2+bx+c的图象如图所示，反比例函数y=
a
x
与正比例函数y=（b+c）x在同一坐标系中的大致图象可能是（　　）
A、
B、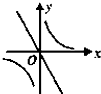
C、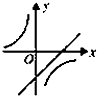
D、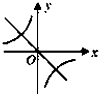
考点：函数的图象
专题：数形结合,函数的性质及应用
分析：先由二次函数的图象确定a，b，c的符号，然后分别判断函数y=
a
x
与y=（b+c）x是否对应即可．
解答： 解：由二次函数的图象可知，a＞0，f（0）=c＜0，f（1）=a+b+c＜0，f（-1）=a-b+c＞0，
对称轴x=-
b
2a
∈(0，1)，
∵a＞0，∴排除C，D．
∵f（1）=a+b+c＜0，
∴b+c＜-a＜0，
即直线y=（b+c）x的斜率小于零，函数y=（b+c）x单调递减，排除A．
故选B．
点评：本题主要考查二次函数图象和性质的应用以及函数图象的识别和判断，考查学生的分析能力．
练习册系列答案
相关题目
已知f（x）是R上的减函数，A（3，-1），B（0，1）是其图象上两个点，则不等式|f（1+lnx）|＜1的解集是
 
．
已知定义在R上的函数f（x）是奇函数且满足f(
3
2
-x)=f(x)，f（-2）=-3，数列{an}满足a1=-1，且
Sn
n
=2×
an
n
+1（其中Sn为{an}的前n项和），则f（a5）+f（a6）=
 
．
已知点的序列An（xn，0），n∈N*，其中x1=0，x2=
1
2
，A3是线段A1A2的中点，A4是线段A2A3的中点，…，An是线段An-2An-1（n≥3）的中点，
（1）写出xn与xn-1，xn-2之间的关系式（n≥3）；
（2）设an=xn+1-xn，求{an}的通项公式．
若a2+b2=
1
4
，a-b=
1
2
，则a+b的值为
 
．
已知函数f（x）=ax2+（b-8）x-a-ab，当x∈（-3，2）时，f（x）＞0，当x∈（-∞，-3）∪（2，+∞）时，f（x）＜0
（1）求a、b的值；
（2）若（c-1）x2+bx+a≤0的解集为R，求实数c的取值范围．
已知实数x，y满足
y≥1
y≤2x-1
x+y≤m
，如果目标函数z=x-y最小值的取值范围为[-2，-1]，则实数m的取值范围
 
．
设x，y为正实数，且x+2y=1，则
1
x
+
1
y
的最小值为
 
．
设f（x）是定义在R上的奇函数，且对任意实数x，恒有f（x+2）=-f（x），当x∈[0，2]时，f（x）=2x-x2．
（1）求证：f（x）是周期函数；
（2）当x∈[2，4]时，求f（x）的解析式； 
（3）计算f（0）+f（1）+f（2）+…+f（2011）=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网