Question

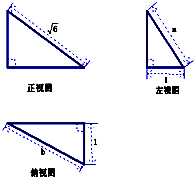
某几何体的三视图如图所示，当a+b取最大值时，这个几何体的体积为（　　）

• A、

  1

  6

• B、

  1

  3

• C、

  2

  3

• D、

  1

  2

Answer 1

考点：由三视图求面积、体积

专题：空间位置关系与距离

分析：三视图复原几何体是长方体的一个角，设出棱长，利用勾股定理，基本不等式，求出最大值．

解答： 解：如图所示，可知AC=

6

，BD=1，BC=b，AB=a．

设CD=x，AD=y，
则x²+y²=6，x²+1=b²，y²+1=a²，
消去x²，y²得a²+b²=8≥

(a+b)2

2

，
所以（a+b）≤4，
当且仅当a=b=2时等号成立，此时x=

3

，y=

3

，
所以V=

1

3

×

1

2

×1×

3

×

3

=

1

2

．
故选D．

点评：本题是基础题，考查几何体的三视图，几何体的表面积和体积的求法，准确判断几何体的形状是解题的关键．