题目内容
函数已知向量
，
的夹角为
，|
|=2，|
|=3，设
=3
-2
，
=2
+k
（1）若
⊥
，求实数k的值；
（2）是否存在实数k，使得
∥
，说明理由．
| a |
| b |
| 2π |
| 3 |
| a |
| b |
| m |
| a |
| b |
| n |
| a |
| b |
（1）若
| m |
| n |
（2）是否存在实数k，使得
| m |
| n |
考点：数量积判断两个平面向量的垂直关系,平行向量与共线向量
专题：平面向量及应用
分析：（1）由已知得
•
=（3
-2
）（2
+k
）=0，由此能求出k=
．
（2）由
∥
，得
=
，由此能求出k．
| m |
| n |
| a |
| b |
| a |
| b |
| 4 |
| 3 |
（2）由
| m |
| n |
| 3 |
| 2 |
| -2 |
| k |
解答：
解：（1）∵向量
，
的夹角为
，|
|=2，|
|=3，
设
=3
-2
，
=2
+k
，
⊥
，
∴
•
=（3
-2
）（2
+k
）
=6
2+（3k-4）
•
-2k
2
=24+6（3k-4）cos
-18k=0，
解得k=
．
（2）∵
∥
，
∴
=
，
解得k=-
．
| a |
| b |
| 2π |
| 3 |
| a |
| b |
设
| m |
| a |
| b |
| n |
| a |
| b |
| m |
| n |
∴
| m |
| n |
| a |
| b |
| a |
| b |
=6
| a |
| a |
| b |
| b |
=24+6（3k-4）cos
| 2π |
| 3 |
解得k=
| 4 |
| 3 |
（2）∵
| m |
| n |
∴
| 3 |
| 2 |
| -2 |
| k |
解得k=-
| 4 |
| 3 |
点评：本题考查实数值的求法，是基础题，解题时要注意向量垂直和向量平行的性质的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
当-
≤x≤
时，函数y=sin x+
cos x的最大值和最小值分别为（ ）
| π |
| 3 |
| π |
| 3 |
| 3 |
| A、1，-1 | ||
B、1，-
| ||
C、2，
| ||
| D、2，0 |
某几何体的三视图如图所示，当a+b取最大值时，这个几何体的体积为（ ）
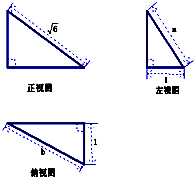
A、
| ||
B、
| ||
C、
| ||
D、
|
某班由24名女生和36名男生组成，现要组织20名学生外参观，若这20名学生按性别分层抽样产生，则参观团的组成法共有（ ）
A、C
| ||||
B、A
| ||||
C、C
| ||||
D、C
|
已知圆上的一段弧长等于该圆的内接正方形的边长，则这段弧所对的圆周角的弧度数为（ ）
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
设f0（x）=ex-e-x，且对任意的n∈N，都有fn+1（x）=fn′（x），则f2013（x）=（ ）
| A、ex-e-x |
| B、e-x-ex |
| C、ex+e-x |
| D、-ex-e-x |