题目内容
已知圆C:(x-1)2+(y-1)2=4,则C上到l:x+y-4=0的距离为
的点有( )个.
| ||
| 2 |
| A、1 | B、2 | C、3 | D、4 |
考点:直线与圆的位置关系
专题:直线与圆
分析:由已知得半径r=2,圆心C(1,1)到直线l:x+y-4=0的距离d=
,由此得到C上到l:x+y-4=0的距离为
的点有2个.
| 2 |
| ||
| 2 |
解答:
解:∵圆C:(x-1)2+(y-1)2=4的圆心C(1,1),
半径r=2,
∴圆心C(1,1)到直线l:x+y-4=0的距离:
d=
=
,
∴C上到l:x+y-4=0的距离为
的点有2个.
故选:B.
半径r=2,
∴圆心C(1,1)到直线l:x+y-4=0的距离:
d=
| |1+1-4| | ||
|
| 2 |
∴C上到l:x+y-4=0的距离为
| ||
| 2 |
故选:B.
点评:本题考查圆C上到l:x+y-4=0的距离为
的点的个数的求法,是中档题,解题时要注意圆的性质的合理运用.
| ||
| 2 |

练习册系列答案
相关题目
当-
≤x≤
时,函数y=sin x+
cos x的最大值和最小值分别为( )
| π |
| 3 |
| π |
| 3 |
| 3 |
| A、1,-1 | ||
B、1,-
| ||
C、2,
| ||
| D、2,0 |
若i为虚数单位,则-i+
=( )
| 1-i |
| 1+i |
| A、-2i | ||
| B、0 | ||
C、
| ||
| D、2i |
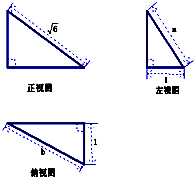
某几何体的三视图如图所示,当a+b取最大值时,这个几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
某班由24名女生和36名男生组成,现要组织20名学生外参观,若这20名学生按性别分层抽样产生,则参观团的组成法共有( )
A、C
| ||||
B、A
| ||||
C、C
| ||||
D、C
|