题目内容
已知不等式丨x-2丨+丨x-a丨＜a的解集非空，求a的取值范围．
考点：绝对值不等式的解法
专题：选作题,不等式
分析：令g（x）=丨x-2丨+丨x-a丨，由绝对值的几何意义可知g（x）min=|2-a|，从而可得实数a的取值范围．
解答：
解：令g（x）=丨x-2丨+丨x-a丨
由绝对值的几何意义得：g（x）=|x-2|+|x-a|≥|2-x+x-a|=|2-a|，
又不等式不等式丨x-2丨+丨x-a丨＜a的解集非空，
∴a＞g（x）min=|2-a|．
∴a＞1．
由绝对值的几何意义得：g（x）=|x-2|+|x-a|≥|2-x+x-a|=|2-a|，
又不等式不等式丨x-2丨+丨x-a丨＜a的解集非空，
∴a＞g（x）min=|2-a|．
∴a＞1．
点评：本题考查绝对值不等式，由绝对值的几何意义得到g（x）min=|2-a|是关键，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
如图是某一四棱锥的三视图，则这个四棱锥的体积为（ ）
| A、4 | B、8 | C、16 | D、20 |
已知函数f（x）是R上的奇函数，且在R上有f′（x）＞0，则f（1）的值 （ ）
| A、恒为正数 | B、恒为负数 |
| C、恒为0 | D、可正可负 |
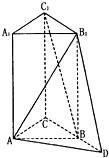已知正三棱柱ABC-A1B1C1中，AA1=2AC=4，延长CB至D，使CB=BD．
直三棱柱ABC-A1B1C1中，AB⊥AC，AC=AA1，AC1与A1C交于一点P，延长B1B到D，使得BD=
如图所示，有三根针和套在一根针上若干金属片．按下列规则，把金属片从一根针上全部移到另一根针上．