题目内容
函数y=x2+1,x∈[-1,2]的值域为 .
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:函数y=x2+1,x∈[-1,2]在[-1,0]上递减,在[0,2]上递增,计算即可得到最值和值域.
解答:
解:函数y=x2+1,x∈[-1,2]
在[-1,0]上递减,在[0,2]上递增,
则x=0取最小为1,x=-1时,y=2,
x=2时,y=5.则最大为5.
则值域为:[1,5].
故答案为:[1,5].
在[-1,0]上递减,在[0,2]上递增,
则x=0取最小为1,x=-1时,y=2,
x=2时,y=5.则最大为5.
则值域为:[1,5].
故答案为:[1,5].
点评:本题考查二次函数在闭区间上的最值,注意对称轴和区间的关系,运用单调性解题,属于基础题和易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知定义在R上的函数f(x)满足f[f(x)]=xf(x)+1,则方程f(x)=0的实根个数为( )
| A、0 | B、1 | C、2 | D、4 |
设f(x-2)=2x,则f(3)的值为( )
| A、64 | B、8 | C、16 | D、32 |
已知函数f(x)=ax2-4ax+c,(a<0),当f(m)≥f(0)时,实数m满足的取值范围是( )
| A、(-∞,0]∪[4,+∞) |
| B、[0,4] |
| C、(0,4) |
| D、(0,+∞) |
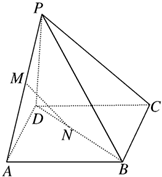 已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.
已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.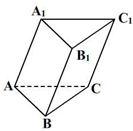 斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成45°角,求这个三棱柱的侧面积.
斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形,侧棱长等于b,一条侧棱AA1与底面相邻两边AB、AC都成45°角,求这个三棱柱的侧面积.