题目内容

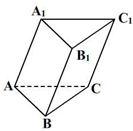斜三棱柱ABC-A1B1C1的底面是边长为a的正三角形，侧棱长等于b，一条侧棱AA1与底面相邻两边AB、AC都成45°角，求这个三棱柱的侧面积．
考点：棱柱、棱锥、棱台的侧面积和表面积
专题：空间位置关系与距离
分析：过点B作BM⊥AA1于M，连结CM，在△ABM和△ACM中，证明ABM≌△ACM，推出AA1⊥面BHC，求出BMC周长，然后求解S侧．
解答： 解：过点B作BM⊥AA1于M，连结CM，在△ABM和△ACM中，
∵AB=AC，∠MAB=∠MAC=45°，MA为公用边，
∴△ABM≌△ACM，∴∠AMC=∠AMB=90°，∴AA1⊥面BHC，
即平面BMC为直截面，
又BM=CM=ABsin45°=
2
2
a，
∴BMC周长为2x
2
2
a+a=（1+
2
）a，且棱长为b，
∴S侧=（1+
2
）ab．
点评：本题考查棱柱的结构特征，侧面积的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
函数y=x2+1，x∈[-1，2]的值域为
 
．
已知函数f（x）=
2x-1
，则该函数的定义域为（　　）
A、{x|x＞
1
2
}
B、{x|x≥
1
2
}
C、{x|x＞-
1
2
}
D、{x|x≥-
1
2
}
现有6道题，其中4道甲类题，2道乙类题，张同学从中任取2道题解答．试求所取的2道题都是甲类题的概率．
设椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2，过F1的直线交椭圆E于A，B两点，满足AF1=2F1B，且AB=3，△ABF2的周长为12．
（1）求AF2；
（2）若cos∠F1AF2=-
1
4
，求椭圆E的方程．
在一次研究性学习中小李同学发现，以下几个式子的值都等于同一个常数M：
①sin213°+cos217°-sin 13°cos 17°=M；
②sin215°+cos215°-sin 15°cos 15°=M；
③sin218°+cos212°-sin 18°cos 12°=M；
④sin2（-18°）+cos248°-sin（-18°）cos 48°=M；
⑤sin2（-25°）+cos255°-sin（-25°）cos 55°=M；
请计算出M值，并将该同学的发现推广为一个三角恒等式．
 
．
已知集合A={x|-3＜x≤5}，集合B={y|-2＜y＜7}，求A∩B、A∪B、（∁RA）∩B．
已知幂函数y=f（x）的图象经过点（2，4），则f（3）为（　　）
A、9B、8C、6D、2
已知点M（3，-2，1），N（3，2，1），则直线MN平行于（　　）
A、y轴B、z轴
C、x轴D、xoz坐标平面

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网