题目内容
设非零向量
,
,
,满足|
|=|
|=|
|,
+
=
,
与
的夹角为( )
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| A、60° | B、90° |
| C、120° | D、150° |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:设
=
,
=
,
=
.由已知条件可得:△ABC为等边三角形,即可得出答案.
| BC |
| a |
| CA |
| b |
| BA |
| c |
解答:
解:设
=
,
=
,
=
.
∵非零向量
,
,
,满足|
|=|
|=|
|,
+
=
,
∴△ABC为等边三角形,
∴
与
的夹角为60°.
故选:A.
| BC |
| a |
| CA |
| b |
| BA |
| c |

∵非零向量
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
∴△ABC为等边三角形,
∴
| b |
| c |
故选:A.
点评:本题考查了向量的加法运算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图所示是一个几何体的三视图,则这个几何体外接球的表面积为( )
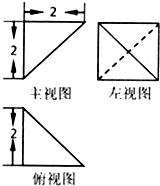

| A、8π | B、12π |
| C、16π | D、48π |
已知等差数列{an}的公差d≠0,Sn是其前n项和,若a22=a1a5,且a6+a9=5a3+3,则
的最大值是( )
| Sn |
| 2n |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
按照如图所示的算法框图,则输出的结果是( )


| A、1005 | B、1006 |
| C、1007 | D、1008 |
已知向量
的模为2
,
=(1,-2),条件p:向量
的坐标为(4,2),条件q:
⊥
,则p是q的( )
| a |
| 5 |
| b |
| a |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |




