题目内容
已知向量
的模为2
，
=（1，-2），条件p：向量
的坐标为（4，2），条件q：
⊥
，则p是q的（ ）
| a |
| 5 |
| b |
| a |
| a |
| b |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据充分条件和必要条件的定义，结合向量垂直和坐标之间的关系，即可得到结论．
解答：
解：若向量
的坐标为（4，2），则
•
=4-2×2=4-4=0，此时
⊥
，即充分性成立．
若
⊥
，设
=（x，y），则x-2y=0，即x=2y，
∵向量
的模为2
，
∴x2+y2=20，
由
，
解得
或
，即
=（4，2）或（-4，-2），
即必要性不成立，
故p是q的充分不必要条件，
故选：A．
| a |
| a |
| b |
| a |
| b |
若
| a |
| b |
| a |
∵向量
| a |
| 5 |
∴x2+y2=20，
由
|
解得
|
|
| a |
即必要性不成立，
故p是q的充分不必要条件，
故选：A．
点评：本题主要考查充分条件和必要条件的判定，利用向量之间的关系是解决本题的关键，比较基础．
练习册系列答案
优等生题库系列答案
相关题目
在△ABC中，∠BAC=60°，点O满足2
+
+
=
，且OC⊥OA，则
的值为（ ）
| OA |
| OB |
| OC |
| 0 |
| AB |
| AC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知实数x，y满足
，则x2+y2+4x+6y+14的最大值为（ ）
|
| A、42 | ||
B、
| ||
C、
| ||
| D、46 |
设非零向量
，
，
，满足|
|=|
|=|
|，
+
=
，
与
的夹角为（ ）
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
| A、60° | B、90° |
| C、120° | D、150° |
已知全集U=R，集合A={x||x-2|＜1}，B={x|y=
}，则A∩B=（ ）
| 4-2x |
| A、（1，2） |
| B、（2，3） |
| C、[2，3） |
| D、（1，2] |
若p：x2-4x+3＞0；q：x2＜1，则p是q的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
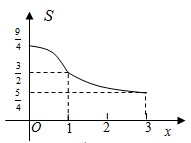
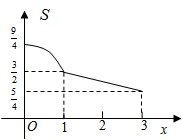
如图在展览厅有一展台，展台是边长为1米的正方体ABCD-A1B1C1D1，面AA1D1D紧靠墙面，一移动光源P在竖直旗杆MN上移动，其中点N在地面上且点N在面BB1C1C上的投影恰好是BC的中点R，MN=3米，NR=2米，设NP=x米，在光源P的照射下，正方体ABCD-A1B1C1D1在面A1B1C1D1紧靠墙面的投影（包括面AA1D1D）的面积为S（x）平方米，则函数y=S（x）的大致图象是（ ）
