题目内容
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老人,结果如下:
(Ⅰ)估计该地区老年人中,需要志愿提供帮助的老年人的比例;
(Ⅱ)通过计算说明,你能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:
K2=
.
| 您是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(Ⅱ)通过计算说明,你能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:
| P(K2≥k) |
| k |
| 0.050 |
| 3.841 |
| 0.010 |
| 6.625 |
| 0.001 |
| 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(Ⅰ)由列联表可知调查的500位老年人中有40+30=70位需要志愿者提供帮助,两个数据求比值得到该地区老年人中需要帮助的老年人的比例的估算值.
(Ⅱ)根据列联表所给的数据,代入随机变量的观测值公式,得到观测值的结果,把观测值的结果与临界值进行比较,看出有多大把握说该地区的老年人是否需要帮助与性别有关.
(Ⅱ)根据列联表所给的数据,代入随机变量的观测值公式,得到观测值的结果,把观测值的结果与临界值进行比较,看出有多大把握说该地区的老年人是否需要帮助与性别有关.
解答:
解:(Ⅰ)调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估计值为
=14%.
(Ⅱ)K2=
≈9.967,
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.
| 70 |
| 500 |
(Ⅱ)K2=
| 500×(40×270-30×160)2 |
| 200×300×70×430 |
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.
点评:本题主要考查统计学知识,考查独立性检验的思想,考查利用数学知识研究实际问题的能力以及相应的运算能力.

练习册系列答案
相关题目
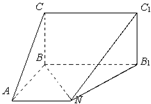 如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,
如图五面体中,四边形CBB1C1为矩形,B1C1⊥平面ABB1N,四边形ABB1N为梯形,且AB⊥BB1,BC=AB=AN=
| 1 |
| 2 |
(1)求证:BN⊥平面C1B1N;
(2)求此五面体的体积.
已知坐标满足方程F(x,y)=0的点都在曲线C上,那么( )
| A、曲线C上的点的坐标都适合方程F(x,y)=0 |
| B、凡坐标不适合F(x,y)=0的点都不在C上 |
| C、不在C上的点的坐标不必适合F(x,y)=0 |
| D、不在C上的点的坐标有些适合F(x,y)=0,有些不适合F(x,y)=0 |
已知函数y=f(x),下列说法错误的是( )
| A、△y=f(x0+△x)-f(x0)叫函数增量 | ||||
B、
| ||||
| C、f(x)在点x0处的导数记为y′ | ||||
| D、f(x)在点x0处的导数记为f′(x0) |
若|z+i|+|z-i|=4,则复平面内与复数z对应的点的轨迹是( )
| A、线段 | B、椭圆 | C、双曲线 | D、圆 |