题目内容
命题“f(x)=loga(x2-ax+1)的值域为R”是真命题,则实数a的取值范围为 .
考点:对数函数的值域与最值
专题:函数的性质及应用
分析:本题是一个对数函数类型,由于函数f(x)的值域是R,所以真数t=x2-ax+1的取值范围应该包含正实数集,利用二次函数值域的理论可得根的判别式大于或等于0,再结合对数的底数必须大于0且不等于1,可得实数a的取值范围.
解答:
解:∵函数f(x)的值域是R,
∴设真数t=x2-ax+1,为关于x的二次函数,设其值域为M,
则必定有(0,+∞)⊆M,
∵二次函数t=x2-ax+1图象是开口向上的抛物线,
∴△=a2-4≥0⇒a2≥4,
又∵对数的底数为a,a>0且a≠1,
∴a≥2,
故答案为:[2,+∞).
∴设真数t=x2-ax+1,为关于x的二次函数,设其值域为M,
则必定有(0,+∞)⊆M,
∵二次函数t=x2-ax+1图象是开口向上的抛物线,
∴△=a2-4≥0⇒a2≥4,
又∵对数的底数为a,a>0且a≠1,
∴a≥2,
故答案为:[2,+∞).
点评:本题的考点是对数型函数的值域与最值,考查对数型函数的值域为全体实数的等价条件的理解,属于中档题.本题是一个易错题,应依据定义理清转化的依据.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
函数f(x)的图象如图所示,下列数值排序正确的是( )
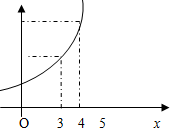

| A、0<f′(3)<f′(4)<f(4)-f(3) |
| B、0<f′(3)<f(4)-f(3)<f′(4) |
| C、0<f′(4)<f′(3)<f(4)-f(3) |
| D、0<f(4)-f(3)<f′(3)<f′(4) |
有一段“三段论”推理:对于可导函数f(x),若f(x)在区间(a,b)上是增函数,则f′(x)>0对x∈(a,b)恒成立,因为函数f(x)=x3在R上是增函数,所以f(x)=3x2>0对x∈R恒成立.以上推理中( )
| A、大前提错误 |
| B、小前提错误 |
| C、推理形式错误 |
| D、推理正确 |
