题目内容
2.函数y=$\frac{|sinx|}{sinx}$+$\frac{|cosx|}{cosx}$+$\frac{|tanx|}{tanx}$的值域是{3,-1}.分析 由已知可得角x的终边不在坐标轴上,分类讨论即可计算得解.
解答 解:由题意可得:sinx≠0,cosx≠0,tanx≠0,角x的终边不在坐标轴上,
当x∈(2kπ,2kπ+$\frac{π}{2}$),k∈Z时,y=$\frac{|sinx|}{sinx}$+$\frac{|cosx|}{cosx}$+$\frac{|tanx|}{tanx}$=1+1+1=3;
当x∈(2kπ+$\frac{π}{2}$,2kπ+π),k∈Z时,y=$\frac{|sinx|}{sinx}$+$\frac{|cosx|}{cosx}$+$\frac{|tanx|}{tanx}$=1-1-1=-1;
当x∈(2kπ+π,2kπ+$\frac{3π}{2}$),k∈Z时,y=$\frac{|sinx|}{sinx}$+$\frac{|cosx|}{cosx}$+$\frac{|tanx|}{tanx}$=-1-1+1=-1;
当x∈(2kπ+$\frac{3π}{2}$,2kπ+2π),k∈Z时,y=$\frac{|sinx|}{sinx}$+$\frac{|cosx|}{cosx}$+$\frac{|tanx|}{tanx}$=-1+1-1=-1.
可得:函数y=$\frac{|sinx|}{sinx}$+$\frac{|cosx|}{cosx}$+$\frac{|tanx|}{tanx}$的值域是{3,-1}.
故答案为:{3,-1}.
点评 本题考查三角函数的值的求法,考查了分类讨论思想,解题时要认真审题,注意三角函数的性质的合理运用,属于基础题.

练习册系列答案
相关题目
13.“a=-1”是“直线x+ay=1与直线ax+y=5平行”的( )条件.
| A. | 充分但不必要 | B. | 必要但不充分 | ||
| C. | 充分 | D. | 既不充分也不必要 |
12.已知f(x)=2sinx+cosx,若函数g(x)=f(x)-m在x∈(0,π)上有两个不同零点α、β,则cos(α+β)=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{3}{5}$ |
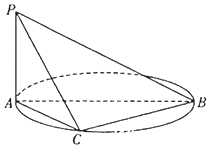 如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.