题目内容
17.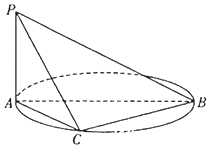 如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.( I)求证:平面PAC⊥平面PBC;
( II)若AC=1,PA=1,求圆心O到平面PBC的距离.
分析 (1)证明AC⊥BC,PA⊥BC,然后证明BC⊥平面PAC,转化证明平面PAC⊥平面PBC.
(2)过A点作AD⊥PC于点D,连BD,取BD的中点E,连OE,说明OE长就是O到平面PBC的距离,然后求解即可.
解答 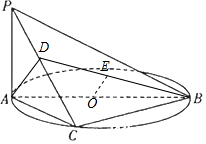 解:(1)证明:由AB是圆的直径得AC⊥BC,
解:(1)证明:由AB是圆的直径得AC⊥BC,
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC
∴BC⊥平面PAC,…(4分)
又∴BC?平面PBC,
所以平面PAC⊥平面PBC…(6分)
(2)过A点作AD⊥PC于点D,则由(1)知AD⊥平面PBC,…(8分)
连BD,取BD的中点E,连OE,则OE∥AD,
又AD⊥平面PBCOE⊥平面PBC,
所以OE长就是O到平面PBC的距离.…(10分)
由中位线定理得$OE=\frac{1}{2}AD=\frac{1}{2}×\frac{PA×AC}{PC}=\frac{{\sqrt{2}}}{4}$…(12分)
点评 本题考查平面与平面垂直的判定定理以及点、线、面距离的求法,考查转化思想以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.点P(-1,2)到直线3x-4y+12=0的距离为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | 1 | D. | 2 |




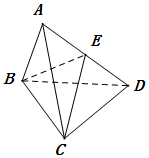 如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.