题目内容
7.设二次函数f(x)=ax2+bx+c(a≠0)的导数为f'(x),f'(0)>0,若?x∈R,恒有f(x)≥0,则$\frac{f(1)}{f'(0)}$的最小值是2.分析 先根据题目的条件建立关于a、b、c的关系式,再结合基本不等式求出最小即可,注意等号成立的条件.
解答 解:∵f(x)=ax2+bx+c
∴f′(x)=2ax+b,f′(0)=b>0
∵对任意实数x都有f(x)≥0
∴a>0,c>0,b2-4ac≤0即 $\frac{4ac}{{b}^{2}}$≥1
则 $\frac{f(1)}{f′(0)}$=$\frac{a+b+c}{b}$=1+$\frac{a+c}{b}$,
而($\frac{a+c}{b}$)2=$\frac{{a}^{2}{+c}^{2}+2ac}{{b}^{2}}$≥$\frac{4ac}{{b}^{2}}$≥1,
∴$\frac{f(1)}{f′(0)}$=$\frac{a+b+c}{b}$=1+$\frac{a+c}{b}$≥2,
故答案为:2.
点评 本题主要考查了导数的运算,以及函数的最值及其几何意义和不等式的应用,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
2.点P(-1,2)到直线3x-4y+12=0的距离为( )
| A. | 5 | B. | $\frac{1}{5}$ | C. | 1 | D. | 2 |
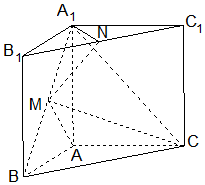 在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.
在三棱柱ABC-A1B1C1中,侧棱与底面垂直,∠BAC=90°,AB=AA1,点M,N分别为A1B 和B1C1的中点.