题目内容
13.“a=-1”是“直线x+ay=1与直线ax+y=5平行”的( )条件.| A. | 充分但不必要 | B. | 必要但不充分 | ||
| C. | 充分 | D. | 既不充分也不必要 |
分析 a=0时,两条直线不平行;a≠0,由两条直线平行可得:-$\frac{1}{a}$=-a,解得a.即可判断出结论.
解答 解:a=0时,两条直线不平行;
a≠0,由两条直线平行可得:-$\frac{1}{a}$=-a,解得a=±1.
∴“a=-1”是“直线x+ay=1与直线ax+y=5平行”的充分不必要条件.
故选:A.
点评 本题考查了两条直线平行的充要条件、简易逻辑的判定方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
8.为推行“新课堂”教学法,某地理老师分别用传统方法和“新课堂”两种不同的教学方法,在甲、乙两个平行班级进行教学实验,为了比较教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,结果如下表:记成绩不低于70分者为“成绩优良”.
(1)由以上统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.025的前提下认为“成绩优良与教学方式有关”?
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$,(n=a+b+c+d)
临界值表:
(2)先从上述40人中,学校按成绩是否优良采用分层抽样的方法抽取8人进行考核,在这8人中,记成绩不优良的乙班人数为X,求X的分布列及数学期望.
| 分数 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100) |
| 甲班频数 | 5 | 6 | 4 | 4 | 1 |
| 乙班频数 | 1 | 3 | 6 | 5 |
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | |||
| 成绩不优良 | |||
| 总计 |
临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
5.已知M是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)左支上一点,A、F分别为双曲线的右顶点和左焦点,且△MAF为等边三角形,则双曲线C的离心率为( )
| A. | 2 | B. | 4 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
3.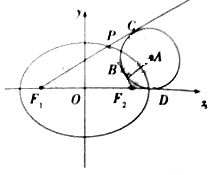 如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )
如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )
 如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )
如图,F1,F2分别是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左,右焦点,椭圆的离心率为$\sqrt{3}$-1,P为椭圆上第一象限内的一点,$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,圆A与△PF1F2三边所在直线都相切,切点分别为B,C,D,则圆A的半径为( )| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{3}$-6 | C. | 4$\sqrt{3}$-2 | D. | 6-2$\sqrt{3}$ |
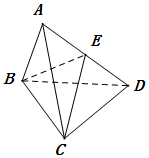 如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.