题目内容
10．从区间[0，1]内任取两个数x，y，则x+y≤1的概率为$\frac{1}{2}$．分析 由题意，本题满足几何概型的概率，利用变量对应的区域面积比求概率即可．
解答 解：在区间[0，1]任取两个数x、y，对应的区域为边长是1的正方形，面积为1，
则满足x+y≤1的区域为三角形，面积为$\frac{1}{2}×1×1$=$\frac{1}{2}$，
由几何概型的公式得到概率P=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 本题考查了几何概型的概率求法；关键是正确选择面积比求概率．
练习册系列答案
阅读快车系列答案
相关题目
5．已知M是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）左支上一点，A、F分别为双曲线的右顶点和左焦点，且△MAF为等边三角形，则双曲线C的离心率为（ ）
| A． | 2 | B． | 4 | C． | $\sqrt{5}$-1 | D． | $\sqrt{5}$+1 |
20．
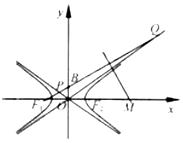如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|=|F1F2|，则双曲线C的渐近线方程是（ ）
如图，F1，F2分别是双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a，b＞0）的左、右焦点，B是虚轴的端点，直线F1B与C的两条渐近线分别交于P，Q两点，线段PQ的垂直平分线与x轴交于点M，若|MF2|=|F1F2|，则双曲线C的渐近线方程是（ ）| A． | y=±x | B． | $y=±\sqrt{3}x$ | C． | $y=±\frac{1}{2}x$ | D． | $y=±\frac{{\sqrt{2}}}{2}x$ |