题目内容
5．已知P为抛物线y2=4x上的任意一点，记点P到y轴的距离为d，对给定点A（3，4），则|PA|+d的最小值为（ ）| A． | $2\sqrt{5}$ | B． | $2\sqrt{5}-1$ | C． | $2\sqrt{5}+1$ | D． | $2\sqrt{5}-2$ |
分析 可设抛物线的焦点为F（1，0），根据抛物线的定义，当|PA|+d最小时，|PA|+|PF|最小，从而问题转化为求|PA|+|PF|的最小值，而由图形便可看出|PA|+|PF|的最小值为|AF|，而|AF|=$2\sqrt{5}$，这样便可得出|PA|+d的最小值．
解答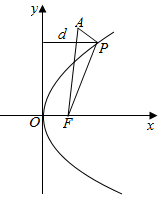 
解：如图，设抛物线焦点F（1，0）；
|PA|+d最小时，|PA|+d+1最小；
根据抛物线的定义，d+1=|PF|；
∴只要求|PA|+|PF|的最小值即可；
由图看出，连接AF，当P点为AF和抛物线交点时，|PA|+|PF|最小；
且最小值为|AF|=$\sqrt{4+16}=2\sqrt{5}$；
∴|PA|+d+1的最小值为$2\sqrt{5}$；
∴|PA|+d的最小值为$2\sqrt{5}-1$．
故选：B．
点评 考查数形结合解题的方法，抛物线的标准方程，根据抛物线的标准方程能求出抛物线的焦点坐标，以及抛物线的定义，两点间的距离公式．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
16．3名医生和6名护士被分配到3所学校为学生检查身体，每个学校分配1名医生和2名护士，不同分配方法共有多少种．（ ）
| A． | 540 | B． | 270 | C． | 180 | D． | 90 |
13．“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查，统计出售价x元和销售量y杯之间的一组数据如下表所示：
通过分析，发现销售量y对奶茶的价格x具有线性相关关系．
（Ⅰ）求销售量y对奶茶的价格x的回归直线方程；
（Ⅱ）欲使销售量为13杯，则价格应定为多少？
注：在回归直线y=$\hat bx+\hat a$中，$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$，$\hat a$=$\overline y$-$\hat b$$\overline x$．$\sum_{i=1}^4{{x_i}^2}={5^2}+{5.5^2}+{6.5^2}+{7^2}$=146.5．
| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
（Ⅰ）求销售量y对奶茶的价格x的回归直线方程；
（Ⅱ）欲使销售量为13杯，则价格应定为多少？
注：在回归直线y=$\hat bx+\hat a$中，$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$，$\hat a$=$\overline y$-$\hat b$$\overline x$．$\sum_{i=1}^4{{x_i}^2}={5^2}+{5.5^2}+{6.5^2}+{7^2}$=146.5．
20．已知圆心在原点，半径为R的圆与△ABC的边有公共点，其中A（4，0），B（6，8），C（2，4），则R的取值范围是（ ）
| A． | $[\frac{{8\sqrt{5}}}{5}，\;10]$ | B． | [4，10] | C． | $[2\sqrt{5}，\;10]$ | D． | $[\frac{{6\sqrt{5}}}{5}，\;10]$ |
10．已知$C_{10}^x=C_{10}^{3x-2}$，则x=（ ）
| A． | 1 | B． | 9 | C． | 1或2 | D． | 1或3 |
