题目内容
16.3名医生和6名护士被分配到3所学校为学生检查身体,每个学校分配1名医生和2名护士,不同分配方法共有多少种.( )| A. | 540 | B. | 270 | C. | 180 | D. | 90 |
分析 三所学校依次选1名医生、2名护士,同一个学校没有顺序,可得不同的分配方法数.
解答 解:三所学校依次选医生、护士,不同的分配方法共有:C31C62C21C42=540种.
故选:A.
点评 本题考查组合及组合数公式,考查计算能力,是基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
4.直线L圆x2+(y-2)2=2相切,且直线L在两坐标轴上的截距相等,则这样的直线L的条数为( )
| A. | .1 | B. | 2 | C. | .3 | D. | .4 |
11.函数y=2sin2x的图象向右平移$\frac{π}{6}$个单位后得到的图象解析式是( )
| A. | $y=2sin(2x+\frac{π}{6})$ | B. | $y=2sin(2x-\frac{π}{6})$ | C. | $y=2sin(2x-\frac{π}{3})$ | D. | $y=2sin(2x+\frac{π}{3})$ |
5.已知P为抛物线y2=4x上的任意一点,记点P到y轴的距离为d,对给定点A(3,4),则|PA|+d的最小值为( )
| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}-1$ | C. | $2\sqrt{5}+1$ | D. | $2\sqrt{5}-2$ |
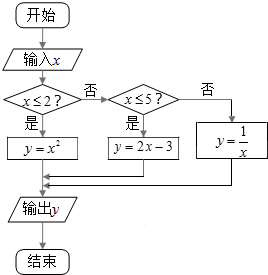 如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.