题目内容
15.已知函数f(x)=x3+x,且f(3a-2)+f(a-1)<0,则实数a的取值范围是(-∞,$\frac{3}{4}$).分析 求函数的导数,判断函数的单调性和奇偶性,将不等式进行转化进行求解即可.
解答 解:函数的导数为f′(x)=3x2+1>0,则函数f(x)为增函数,
∵f(-x)=-x3-x=-(x3+x)=-f(x),
∴函数f(x)是奇函数,
则f(3a-2)+f(a-1)<0等价为f(3a-2)<-f(a-1)=f(1-a),
则3a-2<1-a,
即a<$\frac{3}{4}$,
故答案为:(-∞,$\frac{3}{4}$)
点评 本题主要考查不等式的求解,利用函数奇偶性和单调性之间的关系将不等式进行转化是解决本题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
10.函数f(x)=lnx+2x-7的零点所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
20.某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间Y统计结果如下:
从第一个顾客开始办理业务时计时,据上表估计第三个顾客等待不超过4分钟就开始办理业务的概率为( )
| 办理业务所需的时间Y/分 | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.4 | 0.3 | 0.1 | 0.1 |
| A. | 0.22 | B. | 0.24 | C. | 0.30 | D. | 0.31 |
4.直线L圆x2+(y-2)2=2相切,且直线L在两坐标轴上的截距相等,则这样的直线L的条数为( )
| A. | .1 | B. | 2 | C. | .3 | D. | .4 |
5.已知P为抛物线y2=4x上的任意一点,记点P到y轴的距离为d,对给定点A(3,4),则|PA|+d的最小值为( )
| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}-1$ | C. | $2\sqrt{5}+1$ | D. | $2\sqrt{5}-2$ |
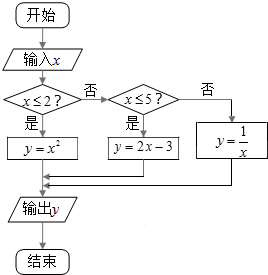 如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应的y的值.