题目内容
13.“奶茶妹妹”对某时间段的奶茶销售量及其价格进行调查,统计出售价x元和销售量y杯之间的一组数据如下表所示:| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
(Ⅰ)求销售量y对奶茶的价格x的回归直线方程;
(Ⅱ)欲使销售量为13杯,则价格应定为多少?
注:在回归直线y=$\hat bx+\hat a$中,$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\bar x\bar y}}}{{\sum_{i=1}^n{x_i^2-n{{\bar x}^2}}}}$,$\hat a$=$\overline y$-$\hat b$$\overline x$.$\sum_{i=1}^4{{x_i}^2}={5^2}+{5.5^2}+{6.5^2}+{7^2}$=146.5.
分析 (1)根据回归系数公式计算回归系数;
(2)把y=13代入回归方程计算x.
解答 解:(Ⅰ)$\overline{x}$=$\frac{5+5.5+6.5+7}{4}$=6,$\overline{y}$=$\frac{12+10+6+4}{4}$=8.
$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=5×12+5.5×10+6.5×6+7×4=182,
$\sum_{i=1}^{4}{{x}_{i}}^{2}$=52+5.52+6.52+72=146.5,
$\stackrel{∧}{b}$=$\frac{182-4×6×8}{146.5-4×{6}^{2}}$=-4,$\stackrel{∧}{a}$=8+4×6=32.
∴销售量y对奶茶的价格x的回归直线方程为$\stackrel{∧}{y}$=-4x+32.
(Ⅱ)令-4x+32=13,解得x=4.75.
答:商品的价格定为4.75元.
点评 本题考查了线性回归方程的解法和数值估计,属于基础题.

练习册系列答案
相关题目
4.直线L圆x2+(y-2)2=2相切,且直线L在两坐标轴上的截距相等,则这样的直线L的条数为( )
| A. | .1 | B. | 2 | C. | .3 | D. | .4 |
5.已知P为抛物线y2=4x上的任意一点,记点P到y轴的距离为d,对给定点A(3,4),则|PA|+d的最小值为( )
| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}-1$ | C. | $2\sqrt{5}+1$ | D. | $2\sqrt{5}-2$ |
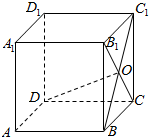 如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.