题目内容
已知函数f(x)=
+
.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性.
| 1 |
| 2x |
| 1 |
| 2 |
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性.
考点:函数奇偶性的判断,函数的定义域及其求法
专题:函数的性质及应用
分析:(1)由2x≠0,得f(x)的定义域为R.
(2)由f(-x)=
+
=2x+
≠±f(x),得f(x)是非奇非偶函数.
(2)由f(-x)=
| 1 |
| 2-x |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵函数f(x)=
+
,
∴2x≠0,解得x∈R,
∴f(x)的定义域为R.
(2)f(-x)=
+
=2x+
≠±f(x),
∴f(x)是非奇非偶函数.
| 1 |
| 2x |
| 1 |
| 2 |
∴2x≠0,解得x∈R,
∴f(x)的定义域为R.
(2)f(-x)=
| 1 |
| 2-x |
| 1 |
| 2 |
| 1 |
| 2 |
∴f(x)是非奇非偶函数.
点评:本题考查函数的定义域和函数的奇偶性的判断,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
设集合A={-1,0,1},B={x∈R|x>0},则A∩B=( )
| A、{-1,0} | B、{-1} |
| C、{0,1} | D、{1} |
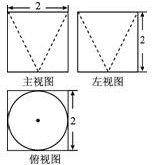
某几何体的三视图如图所示,则它的体积为( )

A、8-
| ||
B、8-
| ||
| C、8-2π | ||
D、
|