题目内容
已知全集U=R,m>0,集合A={x|x2-x-12<0},B={x||x-3|≤m}.
(1)当m=2时,求A∩(∁UB);
(2)命题p:x∈A,命题q:x∈B,若p是q的充分条件,求实数m的取值范围.
(1)当m=2时,求A∩(∁UB);
(2)命题p:x∈A,命题q:x∈B,若p是q的充分条件,求实数m的取值范围.
考点:必要条件、充分条件与充要条件的判断,交、并、补集的混合运算
专题:集合
分析:(1)当m=2时,求出集合A,B,即可求A∩(∁UB);
(2)若p是q的充分条件,建立集合关系即可求实数m的取值范围
(2)若p是q的充分条件,建立集合关系即可求实数m的取值范围
解答:
解:(1)由x2-x-12<0,解得-3<x<4,即A=(-3,4),
当m=2时,B={x||x-3|≤2}={x|1≤x≤5},
则∁UB={x|x>5或x<1},
则A∩(∁UB)={x|-3<x<1},
(2)若p是q的充分条件,则A⊆B,
由m>0知B={x||x-3|≤m}={x|3-m≤x≤3+m},
则
,即
,
即m≥6,
故实数m的取值范围是[6,+∞).
当m=2时,B={x||x-3|≤2}={x|1≤x≤5},
则∁UB={x|x>5或x<1},
则A∩(∁UB)={x|-3<x<1},
(2)若p是q的充分条件,则A⊆B,
由m>0知B={x||x-3|≤m}={x|3-m≤x≤3+m},
则
|
|
即m≥6,
故实数m的取值范围是[6,+∞).
点评:本题主要考查函数的基本运算以及充分条件和必要条件的应用,根据条件求出函数的定义域和值域是解决本题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
函数y=2x+
(x>0)的最小值为( )
| 1 |
| x |
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
下列函数中,在区间(0,5)上为增函数的是( )
A、y=
| ||
| B、y=x2+3 | ||
| C、y=9-x | ||
| D、y=-|x| |
直线l1的斜率为-
,直线l1⊥l2,则l2的斜率为( )
| 1 |
| 2 |
A、-
| ||
| B、1 | ||
C、
| ||
| D、2 |
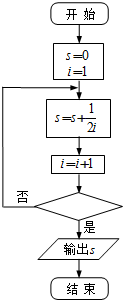 如图给出的是计算
如图给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |
| A、i>8? | B、i>9? |
| C、i>10? | D、i>11? |