题目内容
设点P在曲线y=e2x上，点Q在直线y=2x-3上，则|PQ|的最小值为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：求函数的导数，根据导数的几何意义求出切点坐标，利用平移切线法即可得到结论．
解答：
解：函数y=e2x的导数为f′（x）=2e2x，
由f′（x）=2e2x=2，
得e2x=1，解得x=0，此时y=1，
即当P的坐标为（0，1）时，|PQ|最小，
此时为P到直线2x-y-3=0的距离d=
=
=
，
故答案为：
由f′（x）=2e2x=2，
得e2x=1，解得x=0，此时y=1，
即当P的坐标为（0，1）时，|PQ|最小，
此时为P到直线2x-y-3=0的距离d=
| |-1-3| | ||
|
| 4 | ||
|
4
| ||
| 5 |
故答案为：
4
| ||
| 5 |
点评：本题主要考查两点之间的距离的求解，根据切线的几何意义求出对应的切点是解决本题的关键．
练习册系列答案
相关题目
已知函数f（x）的图象如图所示，则它的一个可能的解析式为（ ）
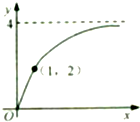
A、y=2
| ||
B、y=2x
| ||
| C、y=log2（x+3） | ||
D、y=4-
|
已知直线l过点P（3，2），且与x轴、y轴的正半轴分别交于A，B两点，如图表所示，则△ABO的面积的最小值为