题目内容
下列函数中,在区间(0,5)上为增函数的是( )
A、y=
| ||
| B、y=x2+3 | ||
| C、y=9-x | ||
| D、y=-|x| |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据增函数的定义对A、B、C、D四个选项进行一一判断;
解答:
解:对于选项A,是反比例函数,在区间(0,5)上为减函数,故不正确;
对于选项B,是开口向上的二次函数,对称轴为y轴,在区间(0,5)上为增函数,故正确;
对于选项C,一次函数y=9-x的一次项系数小于0,则函数在区间(0,5)上为减函数,故不正确;
对于选项D,当x>0时,y=-x,则函数在区间(0,5)上为减函数,故不正确;
故选:B.
对于选项B,是开口向上的二次函数,对称轴为y轴,在区间(0,5)上为增函数,故正确;
对于选项C,一次函数y=9-x的一次项系数小于0,则函数在区间(0,5)上为减函数,故不正确;
对于选项D,当x>0时,y=-x,则函数在区间(0,5)上为减函数,故不正确;
故选:B.
点评:此题主要考查函数的单调性的判断与证明,此题考查的函数都比较简单,是一道基础题.

练习册系列答案
相关题目
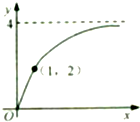
已知函数f(x)的图象如图所示,则它的一个可能的解析式为( )

A、y=2
| ||
B、y=2x
| ||
| C、y=log2(x+3) | ||
D、y=4-
|
在梯形ABCD中,AD∥BC,m是空间直线,则“m⊥AB,m⊥CD”是“m⊥AD,m⊥BC”的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
若f(x)=
,则f(3)=( )
| x+1 |
| A、2 | ||
| B、2或-2 | ||
C、2
| ||
| D、-2 |
“a<-1”是“一元二次方程x2+x+a=0有一个正根和一个负根”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |