题目内容
△ABC的两个顶点B、C的坐标分别为B（-3，0），C（3，0），顶点A到这两个定点的距离的平方和为24，求顶点A的轨迹方程．
考点：轨迹方程
专题：直线与圆
分析：设出点A的坐标，直接由题意列式化简得答案．
解答：
解：设点A的坐标为（x，y），
由题意：|PA|2+|PB|2=24，
即：(
)2+(
)2=24．
化简得：x2+y2=3．
当点A在x轴上时不能形成三角形，
故点P的轨迹方程为x2+y2=3（y≠0）．
由题意：|PA|2+|PB|2=24，
即：(
| (x+3)2+y2 |
| (x-3)2+y2 |
化简得：x2+y2=3．
当点A在x轴上时不能形成三角形，
故点P的轨迹方程为x2+y2=3（y≠0）．
点评：本题考查了轨迹方程，是基础的计算题．
练习册系列答案
相关题目
如果曲线C上任意一点的坐标都是方程F（x，y）=0的解，那么下列命题正确的是（ ）
| A、曲线C的方程是F（x，y）=0 |
| B、曲线C上的点都在方程F（x，y）=0的曲线上 |
| C、方程F（x，y）=0的曲线是C |
| D、以方程F（x，y）=0解为坐标点都在曲线C上 |
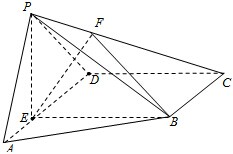如图，在四棱锥P-ABCD中，E为AD上一点，PE⊥平面ABCD，AD∥BC，AD⊥CD，BC=ED=2AE，F为PC上一点，且CF=2FP．