题目内容
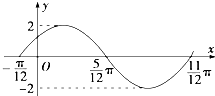 函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|φ|<| π |
| 2 |
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)的图象向右平移
| π |
| 8 |
| 6 |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)直接由五点作图的第一点求得φ值,则函数解析式可求;
(2)由三角函数的图象平移求得函数g(x)的解析式,再由
=
g(x)求得直线y=
与函数y=
g(x)的图象在(0,π)内所有交点的坐标.
(2)由三角函数的图象平移求得函数g(x)的解析式,再由
| 6 |
| 2 |
| 6 |
| 2 |
解答:
解:(1)由五点作图的第一点可知,
2×(-
)+φ=0,解得:φ=
.
∴f(x)=2sin(2x+
);
(2)依题意g(x)=2sin[2(x-
)+
]=sin(2x-
),
由直线y=
与函数y=
g(x)的图象相交得
=2
sin(2x-
),
即sin(2x-
)=
,
∴2x-
=
+2kπ(k∈Z)或2x-
=
+2kπ(k∈Z).
即x=
+kπ或x=
+kπ(k∈Z).
又∵x∈(0,π),故x=
或x=
.
∴交点坐标为(
,
),(
,
).
2×(-
| π |
| 12 |
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
(2)依题意g(x)=2sin[2(x-
| π |
| 8 |
| π |
| 6 |
| π |
| 12 |
由直线y=
| 6 |
| 2 |
| 6 |
| 2 |
| π |
| 12 |
即sin(2x-
| π |
| 12 |
| ||
| 2 |
∴2x-
| π |
| 12 |
| π |
| 3 |
| π |
| 12 |
| 2π |
| 3 |
即x=
| 5π |
| 24 |
| 3π |
| 8 |
又∵x∈(0,π),故x=
| 5π |
| 24 |
| 3π |
| 8 |
∴交点坐标为(
| 5π |
| 24 |
| 6 |
| 3π |
| 8 |
| 6 |
点评:本题考查了利用函数的部分图象求函数解析式,考查了三角函数的图象平移,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
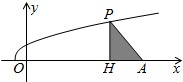 如图,已知点A(11,0),函数y=
如图,已知点A(11,0),函数y= 如图,在半径为1的圆内随机撒100粒豆子,有14粒落在阴影部分,据此估计阴影部分的面积为
如图,在半径为1的圆内随机撒100粒豆子,有14粒落在阴影部分,据此估计阴影部分的面积为