题目内容
各项均为正数的数列{an},其前n项和为Sn,且满足a1>1,6Sn=an2+3an+2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}前n项和为Tn,且满足an+1Tn=anTn+1-9n2-3n+2.问b1为何值时,数列{bn}为等差数列;
(Ⅲ) 求证:
+
+…+
>
(
-
).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{bn}前n项和为Tn,且满足an+1Tn=anTn+1-9n2-3n+2.问b1为何值时,数列{bn}为等差数列;
(Ⅲ) 求证:
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 3 |
| 3n+2 |
| 2 |
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由题意,得6Sn=an2+3an+2,6Sn+1=
+3an+1+2,从而an+1-an=3,由此能求出an=3n-1.(Ⅱ)由已知得
-
=1,数列{
}是以
为首项,以1为公差的等差数列,由此能求出b1=2.(Ⅲ)由
=
=
>
=
,能证明
+
+…+
>
(
-
).
| a | 2 n+1 |
| Tn+1 |
| 3n+2 |
| Tn |
| 3n-1 |
| Tn |
| 3n-1 |
| T1 |
| 2 |
| 1 | ||
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
2(
| ||||
| 3 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 3 |
| 3n+2 |
| 2 |
解答:
(Ⅰ)解:由题意,得6Sn=an2+3an+2①
6Sn+1=
+3an+1+2②
②-①得6an+1=
+3an+1-an2-3an
即(an+1+an)(an+1-an-3)=0…2分
因为an>0,所以an+1-an=3
又n=1时,6a1=a12+3a1+2,
即(a1-1)(a1-2)=0
又a1>1,a1=2
所以an=3n-1.…4分
(Ⅱ)解:由(Ⅰ)及题意,得:
(3n-1)Tn+1-(3n+2)Tn=9n2-3n+2=(3n-1)(3n+2)
即
-
=1,
所以数列{
}是以
为首项,以1为公差的等差数列,…6分
所以
=
+n-1,
即Tn=(
+n-1)(3n-1),
若数列{bn}为等差数列,则
-1=0,即T1=2,
所以b1=2.(此时bn=6n-4)…8分
(Ⅲ)证明:由(Ⅰ)及题意,得:
=
=
>
=
…11分
所以
+
+…+
>
(
-
+
-
+…+
-
)
故
+
+…+
>
(
-
).…13分.
6Sn+1=
| a | 2 n+1 |
②-①得6an+1=
| a | 2 n+1 |
即(an+1+an)(an+1-an-3)=0…2分
因为an>0,所以an+1-an=3
又n=1时,6a1=a12+3a1+2,
即(a1-1)(a1-2)=0
又a1>1,a1=2
所以an=3n-1.…4分
(Ⅱ)解:由(Ⅰ)及题意,得:
(3n-1)Tn+1-(3n+2)Tn=9n2-3n+2=(3n-1)(3n+2)
即
| Tn+1 |
| 3n+2 |
| Tn |
| 3n-1 |
所以数列{
| Tn |
| 3n-1 |
| T1 |
| 2 |
所以
| Tn |
| 3n-1 |
| T1 |
| 2 |
即Tn=(
| T1 |
| 2 |
若数列{bn}为等差数列,则
| T1 |
| 2 |
所以b1=2.(此时bn=6n-4)…8分
(Ⅲ)证明:由(Ⅰ)及题意,得:
| 1 | ||
|
| 1 | ||
|
| 2 | ||
2
|
| 2 | ||||
|
=
2(
| ||||
| 3 |
所以
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 3 |
| 5 |
| 2 |
| 8 |
| 5 |
| 3n+2 |
| 3n-1 |
故
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 2 |
| 3 |
| 3n+2 |
| 2 |
点评:本题考查数列的通项公式的求法,考查等差数列的首项的求法,考查不等式的证明,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某生物研究所进行物种杂交试验,杂交后形成的新生物从出生算起活到3个月的概率为
,活到1年的概率为x,现有一只3个月的这种生物,若它能活到1年的概率为
,则x的值为( )
| 3 |
| 4 |
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若关于x的方程x2+ax-4=0在区间[2,4]上有实数根,则实数a的取值范围是( )
| A、(-3,+∞) |
| B、[-3,0] |
| C、(0,+∞) |
| D、[0,3] |
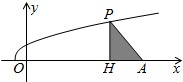 如图,已知点A(11,0),函数y=
如图,已知点A(11,0),函数y=