题目内容
一个盒中有5个球,其中红球1个,黑球2个,白球2个,现从中任取2个球,求下列事件的概率:
(1)求取出2个球是不同颜色的概率;
(2)恰有两个黑球的概率;
(3)至少有一个黑球的概率.
(1)求取出2个球是不同颜色的概率;
(2)恰有两个黑球的概率;
(3)至少有一个黑球的概率.
考点:排列、组合及简单计数问题
专题:概率与统计
分析:列举出满足条件的基本事件共10种,分别找到相应条件的基本事件,根据古典概率公式计算即可
解答:
解:从中任取2个球的基本事件有
=10种,即红黑1,红黑2,红白1,红白2,黑1黑2,黑1白1,黑1白2,黑2白1,黑2白2,白1白2,
(1)从中任取2个球,颜色取出2个球是不同颜色有8种,
故取出2个球是不同颜色的概率P=
=
,
(2)从中任取2个球,恰有两个黑球只有1种情况,故恰有两个黑球的概率为P=
,
(3)从中取2个球,至少有一个黑球的至少有7种情况,故至少有一个黑球的概率为P=
| C | 2 5 |
(1)从中任取2个球,颜色取出2个球是不同颜色有8种,
故取出2个球是不同颜色的概率P=
| 8 |
| 10 |
| 4 |
| 5 |
(2)从中任取2个球,恰有两个黑球只有1种情况,故恰有两个黑球的概率为P=
| 1 |
| 10 |
(3)从中取2个球,至少有一个黑球的至少有7种情况,故至少有一个黑球的概率为P=
| 7 |
| 10 |
点评:本题考查了概率的古典概型求法,属于基础题,应该掌握.

练习册系列答案
相关题目
若关于x的方程x2+ax-4=0在区间[2,4]上有实数根,则实数a的取值范围是( )
| A、(-3,+∞) |
| B、[-3,0] |
| C、(0,+∞) |
| D、[0,3] |
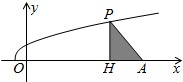 如图,已知点A(11,0),函数y=
如图,已知点A(11,0),函数y= 如图,在半径为1的圆内随机撒100粒豆子,有14粒落在阴影部分,据此估计阴影部分的面积为
如图,在半径为1的圆内随机撒100粒豆子,有14粒落在阴影部分,据此估计阴影部分的面积为