题目内容
9.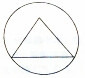 棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )
棱长为a的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,并且图中三角形(正四面体的截面)的面积是3$\sqrt{2}$,则a等于( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 将截面图转化为立体图,求三角形面积就是求正四面体中的△ABD的面积.
解答  解:如图球的截面图就是正四面体中的△ABD,
解:如图球的截面图就是正四面体中的△ABD,
已知正四面体棱长为a
所以AD=$\frac{\sqrt{3}}{2}$a,AC=$\frac{a}{2}$
所以CD=$\sqrt{\frac{3}{4}{a}^{2}-\frac{{a}^{2}}{4}}$=$\frac{\sqrt{2}}{2}$a
截面面积是:$\frac{1}{2}×a×\frac{\sqrt{2}}{2}a=3\sqrt{2}$,
∴a=2$\sqrt{3}$.
故选:C.
点评 本题考查球内接多面体以及棱锥的特征,考查空间想象能力,是中档题.

练习册系列答案
相关题目
8.两个变量y与x的4个不同回归模型中,它们的相关系数r如下,其中拟合效果最好的模型是( )
| A. | 模型2的相关系数r为0.88 | B. | 模型1的相关系数r为-0.99 | ||
| C. | 模型3的相关系数r为0.50 | D. | 模型4的相关系数r为-0.20 |