题目内容
19．在（1-2x）4的展开式中含x3项的系数为-32．分析 写出二项展开式的通项，由x的指数为3得到r值，则答案可求．
解答 解：由${T}_{r+1}={C}_{4}^{r}（-2x）^{r}$=$（-2）^{r}{C}_{4}^{r}{x}^{r}$，
令r=3，得${T}_{4}=-32{x}^{3}$．
∴在（1-2x）4的展开式中含x3项的系数为-32．
故答案为：-32
点评 本题考查二项式系数的性质，熟记二项展开式的通项是关键，是基础题．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
9．
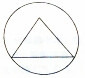棱长为a的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，并且图中三角形（正四面体的截面）的面积是3$\sqrt{2}$，则a等于（ ）
棱长为a的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图所示，并且图中三角形（正四面体的截面）的面积是3$\sqrt{2}$，则a等于（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{3}$ | D． | $\sqrt{3}$ |
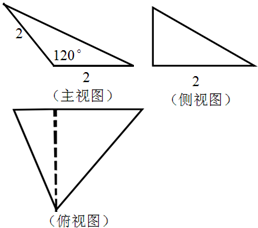某几何体的三视图如图，则该几何体的外接球表面积20π．